早教吧作业答案频道 -->数学-->
(1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.(2)在上面的条件下,点P在BC边上任意运动,延长AP交BQ于点D,请画出图
题目详情
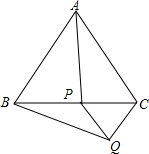
(1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.
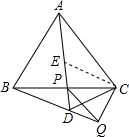
(2)在上面的条件下,点P在BC边上任意运动,延长AP交BQ于点D,请画出图形,问AD与BD+CD之间是否存在确定关系?若存在,请指明这个关系,并证明你的结论;若不存在,请说明理由.
(2)在上面的条件下,点P在BC边上任意运动,延长AP交BQ于点D,请画出图形,问AD与BD+CD之间是否存在确定关系?若存在,请指明这个关系,并证明你的结论;若不存在,请说明理由.

▼优质解答
答案和解析
 (1)∵在等边△ABC中,
(1)∵在等边△ABC中,
∴∠ABC=∠ACB=60°,AC=BC,
∵PQ∥AC,
∴∠CPQ=∠ACB=60°,
∵CQ∥AB,
∴∠PCQ=∠ABC=60°,
∴△PCQ是等边三角形,
∴CP=CQ,
在△ACP与△BQC中,
,
∴△ACP≌△BQC,
∴AP=BQ;
(2)AD=BD+CD,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AC=BC,
∵CQ∥AB,
∴∠QCP=∠ABC=60°,
同理,∠CPQ=60°,
∴△PCQ为等边三角形,
∴CQ=CP,
在△BCQ与△ACP中,
,
∴△BCQ≌△ACP,
∴∠CBQ=∠CAP,
在AP上取点E,使AE=BD,
在△BCD与△ACE中,
,
∴△BCD≌△ACE,
∴CD=CE,∠ACE=∠BCD,
∵∠ACE+∠ECB=60°,
∴∠BCE+∠BCD=∠ECD=60°,
∵CD=CE,
∴△CDE为等边三角形,
∴CD=ED,
∴AD=AE+ED=BD+CD.
 (1)∵在等边△ABC中,
(1)∵在等边△ABC中,∴∠ABC=∠ACB=60°,AC=BC,
∵PQ∥AC,
∴∠CPQ=∠ACB=60°,
∵CQ∥AB,
∴∠PCQ=∠ABC=60°,
∴△PCQ是等边三角形,
∴CP=CQ,
在△ACP与△BQC中,
|
∴△ACP≌△BQC,
∴AP=BQ;
(2)AD=BD+CD,

∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AC=BC,
∵CQ∥AB,
∴∠QCP=∠ABC=60°,
同理,∠CPQ=60°,
∴△PCQ为等边三角形,
∴CQ=CP,
在△BCQ与△ACP中,
|
∴△BCQ≌△ACP,
∴∠CBQ=∠CAP,
在AP上取点E,使AE=BD,
在△BCD与△ACE中,
|
∴△BCD≌△ACE,
∴CD=CE,∠ACE=∠BCD,
∵∠ACE+∠ECB=60°,
∴∠BCE+∠BCD=∠ECD=60°,
∵CD=CE,
∴△CDE为等边三角形,
∴CD=ED,
∴AD=AE+ED=BD+CD.
看了 (1)如图,在等边△ABC中...的网友还看了以下:
在平行四边形ABCD中,E为BC边上一点,连接AE并延长交直线DC于F,且CE=CF.(1)如图1 2020-05-13 …
如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射 2020-06-11 …
如图,在圆O中AB是直径,AT是经过点A的切线,弦CD垂直AB于P点,线段CP的中点为Q,连接BQ 2020-06-12 …
如图,四边形ABCD是正方形,点E在直线BC上,连接AE.将△ABE沿AE所在直线折叠,点B的对应 2020-06-22 …
(2014•东城区一模)如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一 2020-06-30 …
如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C 2020-07-24 …
如图,正方形ABCD的边长是2,M是AD的中点.点E从点A出发,沿AB运动到点B停止.连接EM并延 2020-07-30 …
已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是射线CA上任意一点,DF 2020-11-02 …
如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线 2020-11-03 …
已知椭圆C的方程为x^2/a^2+y^2/b^2=1(a>b>0)的离心率为二分之根号二,且经过M( 2020-11-27 …