早教吧作业答案频道 -->数学-->
已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF.(1)求证:DE=DF;(2)求证:△BDE≌△CDF;(3)求证:AD是BC的中垂线.
题目详情
已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF.
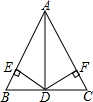
(1)求证:DE=DF;
(2)求证:△BDE≌△CDF;
(3)求证:AD是BC的中垂线.

(1)求证:DE=DF;
(2)求证:△BDE≌△CDF;
(3)求证:AD是BC的中垂线.
▼优质解答
答案和解析
证明:(1)∵AD是△ABC的角平分线,
∴∠EAD=∠FAD.
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°.
在△AED和△AFD中
,
∴△AED≌△AFD.
∴DE=DF.
(2)∵DE⊥AB于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
在△BDE和△CDF中
,
∴△BDE≌△CDF.
(3)∵△AED≌△AFD,
∴AE=AF.
又∵BE=FC,
∴AB=AC.
在△ABD和△ACD中
,
∴△ABD≌△ACD.
∴∠BDA=∠CDA=90°,BD=DC.
∴AD是BC的中垂线.
∴∠EAD=∠FAD.
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°.
在△AED和△AFD中
|
∴△AED≌△AFD.
∴DE=DF.
(2)∵DE⊥AB于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
在△BDE和△CDF中
|
∴△BDE≌△CDF.
(3)∵△AED≌△AFD,
∴AE=AF.
又∵BE=FC,
∴AB=AC.
在△ABD和△ACD中
|
∴△ABD≌△ACD.
∴∠BDA=∠CDA=90°,BD=DC.
∴AD是BC的中垂线.
看了 已知:如图,AD是△ABC的...的网友还看了以下:
证明:a平方+b平方+c平方+d平方大于并且等于-----漫妙的人生无需太多点缀^只求回眸倾城笑( 2020-04-25 …
在正三棱柱ABC-A1B1C1中,AB=4,AA1=根号七,点D是BC中点,点E在AC上,且DE垂 2020-05-17 …
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.(1)求证:B1C∥平面A1 2020-06-15 …
已知平面a垂直于平面b,交线为AB,C属于a,D属于b,AB=AC=BC=4根号3,E为BC的中点 2020-06-27 …
已知b分之a=d分之c,求证:点开看,打不下了-求证a平方分之一+b平方分之一+c平方分之一+d平 2020-07-25 …
平面a交平面b于c,平面a垂直平面d,平面b垂直平面d,求证:平面a垂直平面d 2020-07-30 …
在三棱柱abc-a1b1c1中,点d是ab的中点,求证bc1平行于平面ca1d在三棱柱ABC-A1 2020-07-31 …
1.三棱台ABC-A1B1C1中,AA1垂直于平面ABC,∠BAC=120°,AB=AC=AA1= 2020-07-31 …
已知正三棱柱ABC—A1B1C1若过面对角线AB1与另一面对角线BC1平行的平面交上底面A1B1C 2020-07-31 …
如图,在三棱柱...接上,三棱柱ABC-A'B'C'中,D为BC上一点,且A'B平行于平面AC'D. 2020-11-03 …