已知正三棱柱ABC—A1B1C1若过面对角线AB1与另一面对角线BC1平行的平面交上底面A1B1C1的一边A1C1于点D.(1)确定D的位置并证明你的结论;(2)证明平面AB1D⊥平面AA1D;(3)

Question

已知正三棱柱ABC—A ₁ B ₁ C ₁ 若过面对角线AB ₁ 与另一面对角线BC ₁ 平行的平面交上底面A ₁ B ₁ C ₁ 的一边A ₁ C ₁ 于点D.

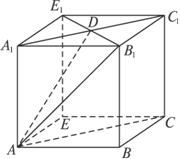
(1)确定D的位置 并证明你的结论;

(2)证明平面AB ₁ D⊥平面AA ₁ D;

(3)若AB∶AA ₁ = 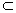求平面AB ₁ D与平面AB ₁ A ₁ 所成角的大小.

Answer 1

剖析:本题的结论是“开放性”的 点D位置的确定如果仅凭已知条件推理难以得出.由于AB1与BC1这两条面对角线是相邻两侧面上的异面直线 于是可考虑将BC1沿BA平行移动 BC1取AE1位置 则平面AB1E1一定平行于BC1 问题可以解决.(1)解:如图 将正三棱柱ABC—A1B1C1补成一直平行六面体ABCE—A1B1C1E1 由AE1∥BC1 AE1平面AB1E1 知BC1∥平面AB1E1 故平面AB1E1应为所求平面 此时平面AB1E1交A1C1于点D 由平行四边形对角线互相平行性质知 D为A1C1的中点.(2)证明:连结AD 从直平行六面体定义知AA1⊥底面A1B1C1D1 且从A1B1C1E1是菱形知 B1E1⊥A1C1 据三垂线定理知 B1E1⊥AD.    又AD∩A1C1=D 所以B1E1⊥平面AA1D.    又B1E1平面AB1D 所以平面AB1D⊥平面AA1D.(3)解:因为平面AB1D∩平面AA1D=AD     所以过A1作A1H⊥AD于点H.    作HF⊥AB1于点F 连结A1F 从三垂线定理知A1F⊥AB1.    故∠A1FH是二面角A1AB1D的平面角.    设侧棱AA1=1 侧棱AB=.    于是AB1==.    在Rt△AB1A1中 A1F===     在Rt△AA1D中 AA1=1 A1D=A1C1= AD==.    则A1H==.    在Rt△A1FH中 sin∠A1FH== 所以∠A1FH=45°.    因此可知平面AB1D与平面AB1A1所成角为45°或135°.讲评:本题主要考查棱柱的性质 以及面面关系、二面角的计算 同时考查空间想象能力和综合运用知识解决问题的能力.