早教吧作业答案频道 -->数学-->
已知a>0,b>0,且a+b=1,用分析法证明(a+)(b+)≥.
题目详情
已知a>0,b>0,且a+b=1,用分析法证明(a+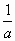 )(b+
)(b+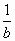 )≥
)≥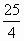 .
.
▼优质解答
答案和解析
答案:
解析:
证明:要证(a+)(b+)≥成立, ∵a>0,b>0, 只需证4a2b2+4(a2+b2)+4-25ab≥0. 又∵a+b=1,只需证4a2b2-33ab+8≥0, 即ab≤或ab≥8成立. ∵a>0,b>0,a+b=1, ∴0<a<1,0<b<1. ∴ab≥8不成立. ∵a+b≥2,即ab≤成立, ∴(a+)(b+)≥成立.
分析:
由(a+)(b+)≥入手探索条件.
提示:
在用分析法证明时,要有必要的文字说明,并在适当的位置应用已知条件.
解析:
证明:要证(a+)(b+)≥成立, ∵a>0,b>0, 只需证4a2b2+4(a2+b2)+4-25ab≥0. 又∵a+b=1,只需证4a2b2-33ab+8≥0, 即ab≤或ab≥8成立. ∵a>0,b>0,a+b=1, ∴0<a<1,0<b<1. ∴ab≥8不成立. ∵a+b≥2,即ab≤成立, ∴(a+)(b+)≥成立.
分析:
由(a+)(b+)≥入手探索条件.
提示:
在用分析法证明时,要有必要的文字说明,并在适当的位置应用已知条件.
看了 已知a>0,b>0,且a+b...的网友还看了以下:
我们把离心率为e=(√5+1)/2的双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)成为我 2020-03-30 …
有如下程序,其输出结果是.#inlcudeintmain(){intx=1,a=0,b=0;swi 2020-06-06 …
已知椭圆x^2/a^2+y^2/b^2=1(a>0,b>0),过点A(a,0)B(b,0)的直线倾 2020-06-23 …
双曲线x2/a2-y2/b2=1(a>0,b>0)的离心率e=2倍根号3/3,过A(0,-b)双曲 2020-07-26 …
双曲线x^2/a^2-y^2/b^2=1(a>0,b>0),双曲线y^2/b^2-x^2/a^2=1 2020-10-31 …
几个简单的数学问题~[知道答案,但我想知道为什么,呵呵.要有过程哈.]1.a>0,b>0,c>0P= 2020-11-01 …
对x,y定义一种新运算,规定:f(x,y)=ax+by2x+y(其中a,b均为非零常数),这里等式右 2020-11-07 …
1、向量m=(a,2),n=(1,b-1),a>0,b>0,m,n的夹角为π/2,求1/a+2/b的 2020-11-24 …
双曲线C:x^2/a^2-y^2/b^2=1(a>0,b>0)两个焦点F1(-c,0),F2(c,0 2020-12-31 …
已知点F是双曲线C:x^2/a^2-y^2/b^2=1(a>0,b>0)的左焦点P为右支上一点直线P 2021-01-11 …