早教吧作业答案频道 -->数学-->
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=π3,BC=212,点F在平面ABED内的正投影为G,且G在AE上,FG=3,点M在线段CF上,且CM=14CF.(1)证明:直线GM∥平面DEF;(2)求三棱锥M-DEF
题目详情
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=
,BC=
,点F在平面ABED内的正投影为G,且G在AE上,FG=
,点M在线段CF上,且CM=
CF.
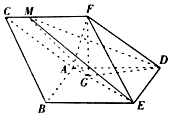
(1)证明:直线GM∥平面DEF;
(2)求三棱锥M-DEF的体积.
| π |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 4 |

(1)证明:直线GM∥平面DEF;
(2)求三棱锥M-DEF的体积.
▼优质解答
答案和解析
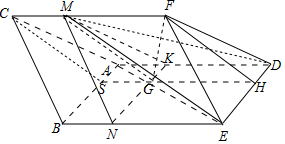
(1)证明:如图,∵面ABED是边长为2的菱形,且∠ABE=
,
∴△ABE为正三角形,且AE=2,
∵FG⊥GE,FG=
,EF=BC=
,
∴EG=
,则AG:HG=1:3,过G作SH∥AD,
交AB于S,交DE于H,
则SG:GH=1:3,
连接CS、FH,∵CM=
CF,∴CM:MF=1:3,
∴MG∥FH,又FH⊂平面DEF,MG⊄平面DEF,
∴直线GM∥平面DEF;
(2) 设过MG且平行于平面DEF的平面交三棱柱于MNK,
得三棱柱DEF-MNK,可得VM-DEF=
VDEF-KMN=VM-NEK,
∵NK=2,NE=
BE=
,∴S△NEK=
×2×
×sin
=
.
则VM-NEK=
×
×
=
.
| π |
| 3 |

∴△ABE为正三角形,且AE=2,
∵FG⊥GE,FG=
| 3 |
| ||
| 2 |
∴EG=
| 3 |
| 2 |
交AB于S,交DE于H,
则SG:GH=1:3,
连接CS、FH,∵CM=
| 1 |
| 4 |
∴MG∥FH,又FH⊂平面DEF,MG⊄平面DEF,
∴直线GM∥平面DEF;
(2) 设过MG且平行于平面DEF的平面交三棱柱于MNK,
得三棱柱DEF-MNK,可得VM-DEF=
| 1 |
| 3 |
∵NK=2,NE=
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 3 |
3
| ||
| 4 |
则VM-NEK=
| 1 |
| 3 |
3
| ||
| 4 |
| 3 |
| 3 |
| 4 |
看了 如图,三棱柱ABC-DEF中...的网友还看了以下:
在△ABC中,D是AB的中点,过D作DE∥BC交AC于E,延长DE到F,使EF=DE,连结AF,C 2020-05-20 …
四边形ABCD是平行四边形,E是对角线AC上一点,射线DE分别交射线CB、AB于点F、G.(1)如 2020-06-12 …
正方形ABCD中,点E在边AB上(点E与A、B不重合)过点E作FG⊥DE,FG与BC交于F,与边D 2020-06-12 …
如图,正方形ABCD中,将∠BAD绕点A顺时针旋转,角的两边分别交CD边于点E,CB边的延长线点F 2020-06-19 …
如图,将▱ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED.(1) 2020-06-19 …
几道数学题目,请教一下平行四边形周长36,一组邻边差为4,求四边形各边长已知平行四边形ABCD对角 2020-07-03 …
(2014•上海)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F, 2020-07-21 …
如图,在三角形ABC中,AB=AC,D是边BC延长线上一点,E是边AC上一点,如果角EBC=角D, 2020-08-01 …
如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.(1 2020-11-03 …
如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,(1)求证: 2020-11-03 …