早教吧作业答案频道 -->数学-->
已知圆C1的参数方程为(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为.(I)将圆C1的参数方程化为普通方程,将圆C2的极坐标方程
题目详情
已知圆C 1 的参数方程为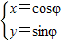 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C 2 的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C 2 的极坐标方程为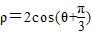 .
.
(I)将圆C 1 的参数方程化为普通方程,将圆C 2 的极坐标方程化为直角坐标方程;
(II)圆C 1 、C 2 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
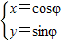 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C 2 的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C 2 的极坐标方程为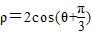 .
.(I)将圆C 1 的参数方程化为普通方程,将圆C 2 的极坐标方程化为直角坐标方程;
(II)圆C 1 、C 2 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
▼优质解答
答案和解析
分析:
(Ⅰ)对于曲线C1利用三角函数的平方关系式sin2φ+cos2φ=1即可;对于曲线C2利用极坐标与直角坐标的互化公式即可化简;(Ⅱ)先求出两圆的圆心距,与两圆的半径和差进行比较即可判断出两圆的位置关系;再将两圆的方程联立求出其交点坐标,利用两点间的距离公式即可.
(I)由得x2+y2=1即为圆C1的普通方程.又∵ρ=2cos(θ+)=cosθ-sinθ,∴ρ2=ρcosθ-ρsinθ.∴x2+y2-x+y=0,即.(II)圆心距,得两圆相交.由两圆的方程联立得,解得或即A(1,0),B,∴.
点评:
熟练掌握极坐标与直角坐标的互化公式、两圆的位置关系判定方法及两点间的距离公式是解题的关键.
分析:
(Ⅰ)对于曲线C1利用三角函数的平方关系式sin2φ+cos2φ=1即可;对于曲线C2利用极坐标与直角坐标的互化公式即可化简;(Ⅱ)先求出两圆的圆心距,与两圆的半径和差进行比较即可判断出两圆的位置关系;再将两圆的方程联立求出其交点坐标,利用两点间的距离公式即可.
(I)由得x2+y2=1即为圆C1的普通方程.又∵ρ=2cos(θ+)=cosθ-sinθ,∴ρ2=ρcosθ-ρsinθ.∴x2+y2-x+y=0,即.(II)圆心距,得两圆相交.由两圆的方程联立得,解得或即A(1,0),B,∴.
点评:
熟练掌握极坐标与直角坐标的互化公式、两圆的位置关系判定方法及两点间的距离公式是解题的关键.
看了 已知圆C1的参数方程为(φ为...的网友还看了以下:
已知曲线C1的参数方程为x=4+5cost,y=5+5sint,以坐标原点为极点,x轴的正半轴为极 2020-06-14 …
曲线C1的参数方程为x=2+2cosαy=2sinα(α为参数),以坐标原点O为极点,x轴正半轴为 2020-07-09 …
已知平面直角坐标系xOy,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为,曲线C的极 2020-07-19 …
在极坐标系中,过点M(2,0)的直线l与极轴的夹角α=π3(Ⅰ)将l的极坐标方程写成ρ=f(θ)的 2020-07-31 …
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为(2,π 2020-07-31 …
已知曲线C1的直角坐标方程为x24+y2=1,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系, 2020-07-31 …
在直角坐标系xOy中,圆C的方程为(x-1)2+y2=12,以坐标原点为极点,x轴的正半轴为极轴建 2020-07-31 …
在直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,已知△ABC三个在直角坐标系x 2020-07-31 …
选修4-4:坐标系与参数方程选讲.在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为(2,π3 2020-07-31 …
已知曲线C1的方程为x2+y2-8x-10y+16=0.以坐标原点为极点,x轴的正半轴为极轴建立极坐 2020-10-31 …