早教吧作业答案频道 -->数学-->
已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.(1)若点N(0,2),求点M的坐标;(2)探究直线MN是否过定点,若过定点,求出该定点;若不存在,请
题目详情
已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.
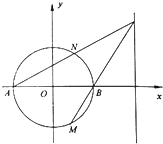
(1)若点N(0,2),求点M的坐标;
(2)探究直线MN是否过定点,若过定点,求出该定点;若不存在,请说明理由.

(1)若点N(0,2),求点M的坐标;
(2)探究直线MN是否过定点,若过定点,求出该定点;若不存在,请说明理由.
▼优质解答
答案和解析
 (1)因为点N(0,2),A(-2,0),
(1)因为点N(0,2),A(-2,0),
所以直线AN的方程为y=x+2,
令x=4,则P(4,6),
又因为B(2,0),
所以直线BP的方程为y=3(x-2),
由y=3(x-2)及x2+y2=4,
解得M(
,-
);
(2)设P(4,t),因为点A(-2,0),
所以直线AN的方程为y=
(x+2),
由y=
(x+2)及x2+y2=4,解得N(
,
),
因为点B(2,0),所以直线BM的方程为y=
(x-2),
由y=
(x-2)及x2+y2=4,解得M(
,
),
过定点C(1,0),因为kNC=
=
,
kMC=
=
,
所以kNC=kMC,
所以M,N,C三点共线,
所以直线MN恒过定点C(1,0).
 (1)因为点N(0,2),A(-2,0),
(1)因为点N(0,2),A(-2,0),所以直线AN的方程为y=x+2,
令x=4,则P(4,6),
又因为B(2,0),
所以直线BP的方程为y=3(x-2),
由y=3(x-2)及x2+y2=4,
解得M(
| 8 |
| 5 |
| 6 |
| 5 |
(2)设P(4,t),因为点A(-2,0),
所以直线AN的方程为y=
| t |
| 6 |
由y=
| t |
| 6 |
| 72-2t2 |
| 36+t2 |
| 24t |
| 36+t2 |
因为点B(2,0),所以直线BM的方程为y=
| t |
| 2 |
由y=
| t |
| 2 |
| 2t2-8 |
| 4+t2 |
| -8t |
| 4+t2 |
过定点C(1,0),因为kNC=
| ||
|
| 8t |
| 12-t2 |
kMC=
| ||
|
| -8t |
| t2-12 |
所以kNC=kMC,
所以M,N,C三点共线,
所以直线MN恒过定点C(1,0).
看了 已知圆O:x2+y2=4交x...的网友还看了以下:
函数f(x)=2lnx - x² - kx(k∈R),若函数f(x)存在两个零点m,n(0<m<n 2020-05-13 …
已知二次函数y=ax^2+(b+1)x+(b-1),若存在x0∈R,是关于x的方程ax^2+(b+ 2020-06-02 …
设函数f(x)二阶可导且满足恒等式:xf''(x)+(1-x)f'(x)=e^x-1若f(x)以x 2020-06-12 …
已知P是椭圆x^2/4y^2/3=1上的一点,F1,F2是该椭圆的两个焦点,若三角形PF1F2的内 2020-07-20 …
已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N 2020-07-30 …
求直线L是否过X轴上的一定点,若过定点,给出证明,并求出该定点;若不过,请说明理由.直线L[(2- 2020-07-31 …
若D点的坐标4,3,点P是X轴正半轴上的动点,点Q是反比例函数Y=12/X(X>0)图像的动点,若 2020-08-03 …
怎么证明一个函数的不动点包含稳定点对于函数f(x),若有f(x)=x则称x为该函数的"不动点",若f 2020-10-30 …
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点.若一个多边形的顶点全是格点 2020-11-18 …
二次函数题,好难``````````抛物线y=ax^2+2p-q^2(^为乘方)与y轴交C点,与x轴 2020-12-23 …