早教吧作业答案频道 -->数学-->
已知O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交O于点D(1)如图1,求证:BD=ED;(2)如图2,AD为O的直径.若BC=6,sin∠BAC=35,求OE的长.
题目详情
已知 O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交 O于点D
(1)如图1,求证:BD=ED;
(2)如图2,AD为 O的直径.若BC=6,sin∠BAC=
,求OE的长.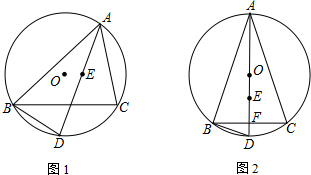
(1)如图1,求证:BD=ED;
(2)如图2,AD为 O的直径.若BC=6,sin∠BAC=
| 3 |
| 5 |

▼优质解答
答案和解析
(1)证明:连接BE.
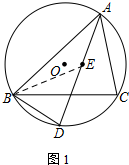
∵是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠DBC=∠CAD.
∴∠DBC=∠BAC.
∵∠BED=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴BD=ED.
(2)如图2所示;连接OB.
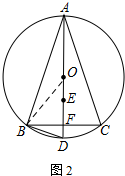
∵AD是直径,A平分∠BAC,
∴AD⊥BC,且BD=FC=3.
∵∠BAC=∠BOD,sin∠BAC=
,BF=3,
∴OB=5.
∵在Rt△BOF中,BF=3,OB=5,
∴OF=
=4.
∴DF=1.
在Rt△BDF中,BF2+DF2=BD2.
∴BD=
.
∴DE=
.
使用OE=5-
.

∵是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠DBC=∠CAD.
∴∠DBC=∠BAC.
∵∠BED=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴BD=ED.
(2)如图2所示;连接OB.

∵AD是直径,A平分∠BAC,
∴AD⊥BC,且BD=FC=3.
∵∠BAC=∠BOD,sin∠BAC=
| 3 |
| 5 |
∴OB=5.
∵在Rt△BOF中,BF=3,OB=5,
∴OF=
| OB2-BF2 |
∴DF=1.
在Rt△BDF中,BF2+DF2=BD2.
∴BD=
| 10 |
∴DE=
| 10 |
使用OE=5-
| 10 |
看了 已知O为△ABC的外接圆,点...的网友还看了以下:
a是b的倍数,c是a的倍数(a、c不相同),下列判断错误的是()A、a与b的和也一定是b的倍数B、a 2020-03-30 …
一个整式与多项式x的平方减y的平方的差为x的平方加y的平方,则这个整式为()一个整式与多项式x的平 2020-04-22 …
若X^2a+b-2X^a-b+3=o是关于X的一元二次方程,求a、b的值.张敏是这样考虑的:满足条 2020-04-26 …
在长和宽分别是a,b的矩形纸片的四个角都减去一个边长为x的正方形,折起来做成一个没有盖的盒子(1) 2020-05-13 …
在探究“影响滑动摩擦力大小的因素”的实验中.(1)为了探究滑动摩擦力与速度大小的关系 在不同速度下 2020-05-16 …
《我身上裹着的是我的父母》阅读答案北极,被称为世界的冰窖.在这儿,生活着一种浑身长满绒毛的鸟儿—— 2020-05-16 …
函数y=x^2+bx-4在(-无穷,-1)上是递减的,在[-1,+无穷]上是递增的,则b的符号为( 2020-05-17 …
动脑筋答题a的平方+b的平方=c的平方3的平方+4的平方=5的平方5的平方+12的平方=13的平方 2020-05-20 …
在直角坐标系中,已知线段AB,点A的坐标为(1,-2),点B的坐标为(3,0),如图1所示.(1) 2020-06-14 …
如图,已知一次函数y=kx+b的图像与反比例函数y=8/x的图像交于A,B如图所示,已知一次函数y 2020-06-14 …