H为锐角三角形ABC的垂心，在线段CH上任取一点E，延长CH到F，使HF=CE，作FD⊥BC，EG⊥BH，其中D，G为垂足，M是线段CF的中点，O1，O2分别△ABG，△BCH的外接圆圆心，O1，O2的另一交点为N；证明：

Question

H为锐角三角形ABC的垂心，在线段CH上任取一点E，延长CH到F，使HF=CE，作FD⊥BC，EG⊥BH，其中D，G为垂足，M是线段CF的中点，O₁，O₂分别△ABG，△BCH的外接圆圆心， O₁， O₂的另一交点为N；证明：

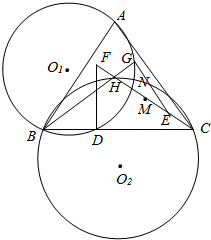
（1）A，B，D，G四点共圆；
（2）O₁，O₂，M，N四点共圆．

Answer 1

证明：（1）如图，设EG∩DF=K，连接AH，

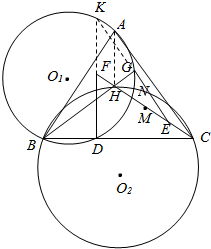
∵AC⊥BH，EK⊥BH，AH⊥BC，KF⊥BC，
∴AC∥EK，AH∥KF，且CH=EF，
∴△CAH≌△EKF，
∴AH与KF平行且相等，
故AK∥HF，
∴∠KAB=90°=∠KDB=∠KGB，
∴A，B，D，G四点共圆；
（2）由（1）得：BK为圆O₁的直径，作圆O₂的直径BP，连接CP，KP，HP，O₁O₂，

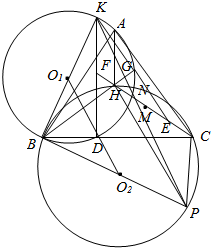
则∠BCP=∠BHP=90°，
∴CP∥AH，HP∥AC，
故AHPC为平行四边形，
进而PC=KF，且PC∥KF，
故KP与CF互相平分于M，
故O₁，O₂，M分别是△KBP三边的中点，
∴KM∥O₁O₂，
而由∠KNB=90°，O₁O₂⊥KN，
∴N，M，K三点共线，
∴MN∥O₁O₂，
根据三角形中位线定理可得：
MO₂=O₁B=O₁N，
因此四边形O₁O₂MN为梯形．
故O₁，O₂，M，N四点共圆．