早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的O与边BC相切于点E.(1)若AC=5,BC=13,求O的半径;(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
题目详情
如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的 O与边BC相切于点E.
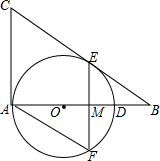
(1)若AC=5,BC=13,求 O的半径;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.

(1)若AC=5,BC=13,求 O的半径;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
▼优质解答
答案和解析
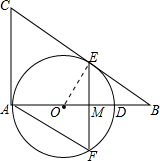 (1) 连接OE,设圆O半径为人,
(1) 连接OE,设圆O半径为人,
在Rt△ABC中,BC=13,AC=5,
根据勾股定理得:AB=
=12,
∵BC与圆O相切,
∴OE⊥BC,
∴∠OEB=∠BAC=90°,
∵∠B=∠B,
∴△BOE∽△BCA,
∴
=
,即
=
,
解得:r=
;
(2)∵
=
,∠F=2∠B,
∴∠AOE=2∠F=4∠B,
∵∠AOE=∠OEB+∠B,
∴∠B=30°,∠F=60°,
∵EF⊥AD,
∴∠EMB=∠CAB=90°,
∴∠MEB=∠F=60°,CA∥EF,
∴CB∥AF,
∴四边形ACEF为平行四边形,
∵∠CAB=90°,OA为半径,
∴CA为圆O的切线,
∵BC为圆O的切线,
∴CA=CE,
∴平行四边形ACEF为菱形.
 (1) 连接OE,设圆O半径为人,
(1) 连接OE,设圆O半径为人,在Rt△ABC中,BC=13,AC=5,
根据勾股定理得:AB=
| BC2-AC2 |
∵BC与圆O相切,
∴OE⊥BC,
∴∠OEB=∠BAC=90°,
∵∠B=∠B,
∴△BOE∽△BCA,
∴
| OE |
| AC |
| BO |
| BC |
| r |
| 5 |
| 12-r |
| 13 |
解得:r=
| 10 |
| 3 |
(2)∵
 |
| AE |
 |
| AE |
∴∠AOE=2∠F=4∠B,
∵∠AOE=∠OEB+∠B,
∴∠B=30°,∠F=60°,
∵EF⊥AD,
∴∠EMB=∠CAB=90°,
∴∠MEB=∠F=60°,CA∥EF,
∴CB∥AF,
∴四边形ACEF为平行四边形,
∵∠CAB=90°,OA为半径,
∴CA为圆O的切线,
∵BC为圆O的切线,
∴CA=CE,
∴平行四边形ACEF为菱形.
看了 如图,在Rt△ABC中,∠B...的网友还看了以下:
按要求连接方格.以下几种情况我们都认为是方格相连.观察下面方格里的数,按要求(同时满足以下两点)连接 2020-03-30 …
(2013•海南)(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E 2020-06-11 …
在空间有n个点分别标记为点1234……n任意两点间均用一电阻为R的导线相连接再把一和点n接到电动势 2020-06-14 …
在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B、C重合),连接AD,将AD绕点 2020-06-25 …
利用两个相同的单刀双掷开关A和B,小明设计了一个电路,使电动机通过控制开关的操作,既能正转,也能反 2020-07-22 …
已知,在正方形ABCD中,点P是射线AD上一动点(不与D重合),连接BP,在BP的右侧作等腰直角三 2020-07-30 …
直线y=-x+2与x轴、y轴分别交于A和B,C(1,0)是x轴上的点(1)点M是线段OB上一点.连接 2020-12-05 …
在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N.(1) 2020-12-05 …
在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N.(1) 2020-12-05 …
1.抛物线y=(k-1)x∧2+(2-2k)x+1,无论k取何值它必经的一点()2.已知三角形ABC 2020-12-21 …