早教吧作业答案频道 -->数学-->
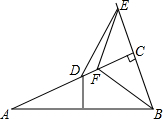
如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
题目详情
如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

▼优质解答
答案和解析
DE=BF,DE⊥BF.理由如下: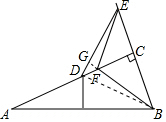
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
在△ECD和△FCB中,
,
∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,
∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.

连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
在△ECD和△FCB中,
|
∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,
∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
1.3吨=()千克4分之3小时=()分在直径是3米的圆形彭水池边上每隔0.628米放一盆花,一共可 2020-04-15 …
设抛物线y^2=2px(p>0)的焦点F,准线L,A.B是抛物线上不同的两点(1)若OA⊥OB(O 2020-05-13 …
直线把梯形分成面积相等的两部分在直角梯形ABCD中,∠C=∠D=90°,AD=4,BC=CD=2, 2020-05-16 …
钢丝绳磨损(或腐蚀)部分在直径的40%以内者可降级使用。( ) 2020-05-30 …
情景观察将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别 2020-06-11 …
已知面a,b,r,满足a垂直于r,b垂直于r,a交b=l,求证:l垂直于r已知面a,b,r,满足a 2020-07-12 …
如图在长方体ABCD-A1B1C1D1中,P,Q,R分别为BC,CD,CC'的中点.(1)判断直线 2020-07-20 …
如图所示,光滑管道AB部分平直,BC部分为竖直半圆环,圆环半径为R.现有一个质量为m半径为r(r< 2020-07-21 …
在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1, 2020-07-25 …
关于球和直角坐标变幻的题!有一用球坐标表示的场E(矢量)=er(r是角标)25/r*r求在直角坐标 2020-08-03 …