早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.(1)求矩形OABC的对角线的长;(2)求点B的坐标;(3)求△EOB的面积.
题目详情
如图,在平面直角坐标系中,有一矩形OABC,OA=8,OC=6,过点D(0,6)作y轴的垂线交OA于点E,点B恰在这条直线上.
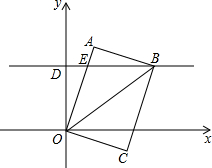
(1)求矩形OABC的对角线的长;
(2)求点B的坐标;
(3)求△EOB的面积.

(1)求矩形OABC的对角线的长;
(2)求点B的坐标;
(3)求△EOB的面积.
▼优质解答
答案和解析
(1)∵四边形OABC是矩形,
∴AB=OC=6,∠A=90°,
∴OB=
=
=10,
即矩形OABC的对角线的长为10;
(2)∵BD⊥OD,
∴∠ODB=90°,
∴BD=
=
=8,
∴点B的坐标为(8,6);
(3)∵OD=6,AB=6,
∴OD=AB,
在Rt△OBD和Rt△BOA中,
,
∴Rt△OBD≌Rt△BOA(HL),
∴∠OBD=∠BOA,
∴OE=BE,
设OE=BE=x,则DE=8-x,
在Rt△ODE中,由勾股定理得:62+(8-x)2=x2,
解得:x=
,即BE=
,
∴△EOB的面积=
BE•OD=
×
×6=
.
∴AB=OC=6,∠A=90°,
∴OB=
| OA2+AB2 |
| 82+62 |
即矩形OABC的对角线的长为10;
(2)∵BD⊥OD,
∴∠ODB=90°,
∴BD=
| OB2-OD2 |
| 102-62 |
∴点B的坐标为(8,6);
(3)∵OD=6,AB=6,
∴OD=AB,
在Rt△OBD和Rt△BOA中,
|
∴Rt△OBD≌Rt△BOA(HL),
∴∠OBD=∠BOA,
∴OE=BE,
设OE=BE=x,则DE=8-x,
在Rt△ODE中,由勾股定理得:62+(8-x)2=x2,
解得:x=
| 25 |
| 4 |
| 25 |
| 4 |
∴△EOB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 4 |
| 75 |
| 4 |
看了 如图,在平面直角坐标系中,有...的网友还看了以下:
若曲线C上的点到直线的距离比它到点F的距离大1,(1)求曲线C的方程。(2)过点F(1,0)作倾斜 2020-05-15 …
已知直线l:y=kx+1交曲线C:y=ax^2(a>0)于P、Q两点,M为PQ中点,分别过P、Q两 2020-05-15 …
动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4. 2020-06-05 …
已知点F1、F2为双曲线C:x2-y2b2=1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交 2020-06-16 …
椭圆、抛物线以椭圆E:(x^2)/4+y^2=1的上顶点为焦点的抛物线C的标准方程为x^2=2py 2020-06-21 …
已知曲线C上的动点P(x,y)满足到点F(0,1)的距离比到直线y=-2的距离小1.(1)求曲线C 2020-07-20 …
P为双曲线C上一点,F1、F2是双曲线C的两个焦点,过双曲线C的一个焦点作∠F1PF2的平分线的垂 2020-07-21 …
(2014•宁波模拟)已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.(Ⅰ 2020-07-21 …
已知抛物线C:x2=4y.(1)若点P(x0,y0)是抛物线C上一点,求证:过点P的抛物线C的切线 2020-07-22 …
用尺规作图,已知三边作三角形,用到的基本作图是()A.作一个角等于已知角B.作已知直线的垂线C.作 2020-08-02 …