已知函数f（x）=e2x-ax2+bx-1，其中a，b∈R，e为自然对数的底数，若f（1）=0，f′（x）是f（x）的导函数，函数f′（x）在区间（0，1）内有两个零点，则a的取值范围是（）A.（e2-3，e2+1）B.

Question

已知函数f（x）=e^2x-ax²+bx-1，其中a，b∈R，e为自然对数的底数，若f（1）=0，f′（x）是f（x）的导函数，函数f′（x）在区间（0，1）内有两个零点，则a的取值范围是（　　）

A. （e²-3，e²+1）

B. （e²-3，+∞）

C. （-∞，2e²+2）

D. （2e²-6，2e²+2）

Answer 1

∵f（1）=0，∴e²-a-b-1=0，即b=e²-a-1，
∴f（x）=e^2x-ax²+（e²-a-1）x-1，
∴f′（x）=2e^2x-2ax+e²-a-1，
令f′（x）=0得2e^2x=2ax+a+1-e²，
∵函数f′（x）在区间（0，1）内有两个零点，
∴y=2e^2x与y=2ax+a+1-e²的函数图象在（0，1）上有两个交点，
作出y=2e^2x与y=2ax+a+1-e²的函数图象，如图所示：

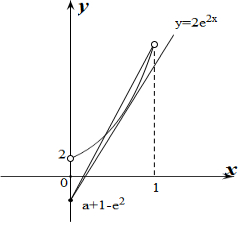
当a+1-e²≥2即a≥e²+1时，直线y=2ax与y=2e^2x最多只有1个交点，不符合题意；
∴a+1-e²<2，即a2+1，
排除B，C，D．
故选A．