早教吧作业答案频道 -->数学-->
如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD向点D运动;点Q从点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达
题目详情
如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD向点D运动;点Q从点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达点D时,点Q也停止运动,连接BP,过点P作BP的垂线交过点Q平行于CD的直线l于点E,BE于CD相交于点F,连接PF,设点P运动时间为t(s),△BPE的面积记为S,
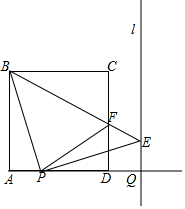
(1)求∠PBE的度数,求S(用含t的代数式表示);
(2)当t为何值时,△PQF是以PF为腰的等腰三角形?
(3)试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.

(1)求∠PBE的度数,求S(用含t的代数式表示);
(2)当t为何值时,△PQF是以PF为腰的等腰三角形?
(3)试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
▼优质解答
答案和解析
(1)如图1中,
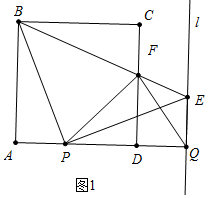
∵四边形ABCD是正方形,
∴AB=AD,∠A=90°,
∵AP=DQ,
∴AD=PQ=AB,
∵PB⊥PE,
∴∠BPE=90°,
∴∠ABP+∠APB=90°,∠APB+∠EPQ=90°,
∴∠ABP=∠EPQ,
在△ABP和△QPE中,
,
∴△ABP≌△QPE,
∴PB=PE,
∴∠PBE=∠PEB=45°.
(2)如图2中,
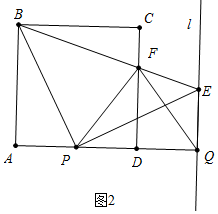
①当AP=PD时,
∵AP=DQ,
∴DP=DQ,
∵FD⊥PQ,
∴PF=FQ,
∴△PFQ是等腰三角形,此时t=2.
②当点P与点D重合时,PF=CD=AD=DQ,△PFQ是等腰三角形,此时t=4.
综上所述,t=2s或4s时,△PFQ是以PF为腰的等腰三角形.
(3)如图3中,△PDF的周长是定值.
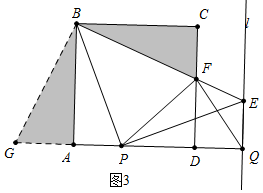
将△BCF绕点B顺时针旋转90°得到△BAG.
∵∠PBE=45°,∠ABC=90°,
∴∠ABP+∠CBF=∠ABP+∠ABG=45°,
∴∠PBG=∠PBF,
在△PBG和△PBF中,
,
∴△PBG≌△PBF,
∴PF=PG,
∴PF=PA+AG=PA+CF,
∴△PDF的周长=PF+DP+DF=(PA+DP)+(DF+CF)=AD+CD=8.
∴△PDF的周长为定值.

∵四边形ABCD是正方形,
∴AB=AD,∠A=90°,
∵AP=DQ,
∴AD=PQ=AB,
∵PB⊥PE,
∴∠BPE=90°,
∴∠ABP+∠APB=90°,∠APB+∠EPQ=90°,
∴∠ABP=∠EPQ,
在△ABP和△QPE中,
|
∴△ABP≌△QPE,
∴PB=PE,
∴∠PBE=∠PEB=45°.
(2)如图2中,

①当AP=PD时,
∵AP=DQ,
∴DP=DQ,
∵FD⊥PQ,
∴PF=FQ,
∴△PFQ是等腰三角形,此时t=2.
②当点P与点D重合时,PF=CD=AD=DQ,△PFQ是等腰三角形,此时t=4.
综上所述,t=2s或4s时,△PFQ是以PF为腰的等腰三角形.
(3)如图3中,△PDF的周长是定值.

将△BCF绕点B顺时针旋转90°得到△BAG.
∵∠PBE=45°,∠ABC=90°,
∴∠ABP+∠CBF=∠ABP+∠ABG=45°,
∴∠PBG=∠PBF,
在△PBG和△PBF中,
|
∴△PBG≌△PBF,
∴PF=PG,
∴PF=PA+AG=PA+CF,
∴△PDF的周长=PF+DP+DF=(PA+DP)+(DF+CF)=AD+CD=8.
∴△PDF的周长为定值.
看了 如图,正方形ABCD(四边相...的网友还看了以下:
一只蚂蚁,爬10米长的斜坡,白天向上爬1米,夜间向下滑3分之二米,它从某日早晨开始向上爬,多少天后 2020-05-22 …
在下列有关Windows98文件名的叙述中,错误的是A.系统支持的长文件名可以长达200多个西文字符 2020-05-24 …
在下列有关Windows 98文件名的叙述中,错误的是A.系统支持的长文件名可以长达200多个西文字 2020-05-24 …
在下列有关Windows98文件名的叙述中,错误的是( )。A.系统支持的长文件名可以长达200多个 2020-05-24 …
卷标可以长达11个字符,可以使用()。 2020-05-31 …
如图,在Rt△ABC中,∠ACB=90°,CA=8,CB=6,动点P从C出发沿CA方向,以每秒1个 2020-06-08 …
如图所示,质量M=8kg的长木板放在光滑水平面上,在长木板的右端施加一水平恒力F=8N,当长木板向 2020-06-12 …
下面这段介绍录音笔的文字在表达上有一些毛病,请改正。录音笔的录音时间至少可以长达10小时以上,这对于 2020-12-22 …
下面这段介绍录音笔的文字在表达上有一些毛病,请加以修改(有几处改几处)。录音笔的录音时间至少可以长达 2020-12-22 …
质粒表达方向与基因表达方向不同,基因可以表达吗我在做基因克隆时,选用pET-30a质粒.该质粒表达方 2021-01-07 …