如图，点E，点F分别在菱形ABCD的边AB，AD上，且AE=DF，BF交DE于点G，延长BF交CD的延长线于H，若AFDF=2，则HFBG的值为（）A.23B.712C.12D.512

Question

如图，点E，点F分别在菱形ABCD的边AB，AD上，且AE=DF，BF交DE于点G，延长BF交CD的延长线于H，若

(AF)/(DF)=2，则(HF)/(BG)的值为（　　）

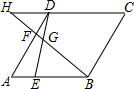
A.

(2)/(3)

B.

(7)/(12)

C.

(1)/(2)

D.

(5)/(12)

Answer 1

∵四边形ABCD是菱形，
∴AB=BC=CD=AD，
∵AF=2DF，设DF=a，则DF=AE=a，AF=EB=2a，
∵HD∥AB，
∴△HFD∽△BFA，
∴(HD)/(AB)=(DF)/(AF)=(HF)/(FB)=(1)/(2)，
∴HD=1.5a，(FH)/(BH)=(1)/(3)，
∴FH=(1)/(3)BH，
∵HD∥EB，
∴△DGH∽△EGB，
∴(HG)/(GB)=(HD)/(EB)=(1.5a)/(2a)=(3)/(4)，
∴(BG)/(HB)=(4)/(7)，
∴BG=(4)/(7)HB，
∴(HF)/(BG)=((1)/(3)EB)/((4)/(7)EB)=(7)/(12)．
故选B．