早教吧作业答案频道 -->数学-->
已知不等式(ax+3)(x2-b)≤0对任意x∈(-∞,0)恒成立,其中a,b是整数,则a+b的取值的集合为{4,10}.
题目详情
已知不等式(ax+3)(x2-b)≤0对任意x∈(-∞,0)恒成立,其中a,b是整数,则a+b的取值的集合为 {4,10} .
▼优质解答
答案和解析
 当b≤0 时,由(ax+3)(x2-b)≤0
当b≤0 时,由(ax+3)(x2-b)≤0
得到ax+3≤0 在x∈(-∞,0)上恒成立,
则a不存在;
当b>0 时,由(ax+3)(x2-b)≤0,
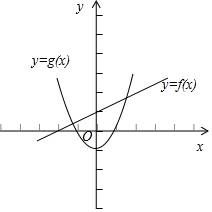
可设f(x)=ax+3,g(x)=x2-b,
又g(x) 的大致图象如下,
那么由题意可知:
再由a,b 是整数得到
或
因此a+b=10或4.
故答案为{4,10}.
 当b≤0 时,由(ax+3)(x2-b)≤0
当b≤0 时,由(ax+3)(x2-b)≤0得到ax+3≤0 在x∈(-∞,0)上恒成立,
则a不存在;
当b>0 时,由(ax+3)(x2-b)≤0,
可设f(x)=ax+3,g(x)=x2-b,
又g(x) 的大致图象如下,
那么由题意可知:
|
再由a,b 是整数得到
|
|
因此a+b=10或4.
故答案为{4,10}.
看了 已知不等式(ax+3)(x2...的网友还看了以下:
设总体X概率密度函数为f(x;θ)=(θ+1)xθ,o<x<1o,其他,其上θ>-1为未知参数.设 2020-06-30 …
设总体X的密度函数为f(x)=θcθx?(θ+1)x>c0...设总体X的密度函数为f(x)=θc 2020-07-09 …
设总体X服从区间(0,θ)上的均匀分布,其中θ>0为未知参数.(X1,X2,…,Xn)是从该总体中 2020-07-11 …
已知函数.(I)判断函数在上的单调性(为自然对数的底);(II)记为的导函数,若函数在区间上存在极 2020-07-20 …
设总体X~N(μ,σ2),其中μ是已知参数,σ2>0是未知参数.(X1,X2,…,Xn)是从该总体 2020-07-20 …
已知函数.(1)若函数f(x)在定义域内为增函数,求实数p的取值范围;(2)当n∈N*时,证明>2 2020-07-22 …
设总体X的密度函数为f(x)=θcθx−(θ+1)x>c0x≤c.其中c>0是已知常数,而θ>1是 2020-07-31 …
设总体X概率密度函数为f(x;θ)=(θ+1)xθ,o<x<1o,其他,其上θ>-1为未知参数.设 2020-07-31 …
设总体X的概率密度为f(x)=xθ2e−x22θ2,x>00,x≤0,,其中θ>0为未知参数.(Ⅰ 2020-07-31 …
定义:对于区间I内可导的函数y=f(x),若∃,使,则称为函数y=f(x)的新驻点.已知函数.(Ⅰ 2020-07-31 …