如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=2；⑤S四边形CDEF=52S△ABF，其中正确的结论有（）A.5个B.4个C.

Question

如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=

√(2)；⑤S_{四边形CDEF}=(5)/(2)S_△ABF，其中正确的结论有（　　）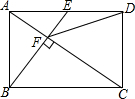

A. 5个

B. 4个

C. 3个

D. 2个

Answer 1

过D作DM∥BE交AC于N，
∵四边形ABCD是矩形，
∴AD∥BC，∠ABC=90°，AD=BC，
∵BE⊥AC于点F，
∴∠EAC=∠ACB，∠ABC=∠AFE=90°，
∴△AEF∽△CAB，故①正确；
∵AD∥BC，
∴△AEF∽△CBF，
∴(AE)/(BC)=(AF)/(CF)，
∵AE=(1)/(2)AD=(1)/(2)BC，
∴(AF)/(CF)=(1)/(2)，
∴CF=2AF，故②正确，
∵DE∥BM，BE∥DM，
∴四边形BMDE是平行四边形，
∴BM=DE=(1)/(2)BC，
∴BM=CM，
∴CN=NF，
∵BE⊥AC于点F，DM∥BE，
∴DN⊥CF，
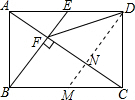
∴DF=DC，故③正确；
设AD=a，AB=b由△BAE∽△ADC，有(b)/(a)=((a)/(2))/(b)．
∵tan∠CAD=(CD)/(AD)=(b)/(a)，
∴tan∠CAD=(√(2))/(2)，故④错误；
∵△AEF∽△CBF，
∴(EF)/(BF)=(AE)/(BC)=(1)/(2)，
∴S_△AEF=(1)/(2)S_△ABF，S_△ABF=(1)/(6)S_矩形ABCD
∴S_△AEF=(1)/(12)S_矩形ABCD，
又∵S_{四边形CDEF}=S_△ACD-S_△AEF=(1)/(2)S_矩形ABCD-(1)/(12)S_矩形ABCD=(5)/(12)S_矩形ABCD，
∴S_{四边形CDEF}=(5)/(2)S_△ABF，故⑤正确；
故选B．