早教吧作业答案频道 -->数学-->
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.(1)求证:BE=AD;(2)用含α的式子表示∠AMB的度数;(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,
题目详情
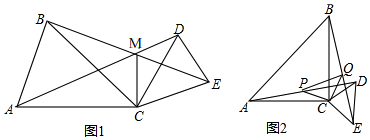
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

▼优质解答
答案和解析
(1)如图1,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)如图1,∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵△ABC中,∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴△ABM中,∠AMB=180°-(180°-α)=α;
(3)△CPQ为等腰直角三角形.
证明:如图2,由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)如图1,∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵△ABC中,∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴△ABM中,∠AMB=180°-(180°-α)=α;
(3)△CPQ为等腰直角三角形.
证明:如图2,由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
|
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
看了 如图①,CA=CB,CD=C...的网友还看了以下:
几道高二不等式证明题.1.a,b属于正数,a不等于b.求证a/根号b+b/根号a>根号a+根号b2. 2020-03-30 …
(1).已知a,b都是正数,且a≠b,求证:2ab/a+b<(ab的开方)(2).已知a,b都是正数 2020-03-30 …
求解几道不等式证明1.求证:x²>4x—5.2.求证:a的四次方+1≥a的三次方+a3.已知a>0 2020-04-27 …
高二上数学不等式【在线等,急】1.求证a²=b²+≥2a+2b2.用作差法求证:1)a²+b²+5 2020-05-13 …
解几个与不等式有关的问题设a,b,c,d均为不等于0的实数,求证:∣b/a∣+∣b/c∣∣c/d∣ 2020-06-06 …
有f(a+b)=f(a)(b),求证:f(0)=1求证:对任意的x属于R,恒有f(x)大于0求证: 2020-06-12 …
不等式证明!1.已知|a|<1,|b|<1,|c|<1.求证:|(a+b+c+abc)/(1+ab 2020-06-12 …
已知:如图∩DAC=∩B求证∩ADC=∩BAC2.已知三角形ABC中,AB为7,BC:AC=4:3 2020-06-27 …
有三道,过程也要写上面.一.求证:小括号里2分之a+b整体的平方小于等于2分之a方加b方二.已知a 2020-08-01 …
在△ABC中∠A,∠B,∠C,所对的边分别是a,b,c,边上的高分别为ha,hb,hc.(1)若a= 2020-12-04 …