早教吧作业答案频道 -->数学-->
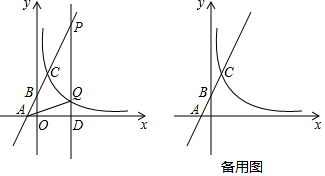
如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A,B,与双曲线y=4x在第一象限内交于点C(1,m),过x轴正半轴上的点D(a,0)作平行于y轴的直线l,分别与直线AB和双曲线y=4x
题目详情
如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A,B,与双曲线y=
在第一象限内交于点C(1,m),过x轴正半轴上的点D(a,0)作平行于y轴的直线l,分别与直线AB和双曲线y=
交于P,Q.
(1)求m和n的值;
(2)当a>1,PQ=2QD时,求△APQ的面积;
(3)当CP=CQ时,求a的值.
| 4 |
| x |
| 4 |
| x |
(1)求m和n的值;
(2)当a>1,PQ=2QD时,求△APQ的面积;
(3)当CP=CQ时,求a的值.

▼优质解答
答案和解析
(1)∵直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=
在第一象限内交于点C(1,m).
∴把C(1,m)代入y=
,得m=4,
∴C(1,4),
把C(1,4)代入y=2x+n中得n=2,
∴m和n的值分别为:4,2;
(2)在y=2x+2中,令y=0,则x=-1,
∴A(-1,0),
∵D(a,0),l∥y轴,
∴P(a,2a+2),Q(a,
),
∵PQ=2QD,
∴2a+2-
=2×
,
解得:a=2,a=-3,
∵点P,Q在第一象限,
∴a=2,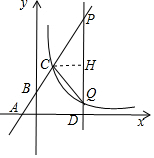
∴PQ=4,
又∵AD=3
∴S△APQ=
×4×3=6;
(3)∵D(a,0),l∥y轴,
∴P(a,2a+2),Q(a,
),
过C作CH⊥PQ于H,
∵C(1,4),
∴H(a,4),
∵PC=CQ,
∴PH=HQ,
∴2a+2-4=4-
,
解得:a=2,a=1(不合题意,舍去),
∴a=2.
| 4 |
| x |
∴把C(1,m)代入y=
| 4 |
| x |
∴C(1,4),
把C(1,4)代入y=2x+n中得n=2,
∴m和n的值分别为:4,2;
(2)在y=2x+2中,令y=0,则x=-1,
∴A(-1,0),
∵D(a,0),l∥y轴,
∴P(a,2a+2),Q(a,
| 4 |
| a |
∵PQ=2QD,
∴2a+2-
| 4 |
| a |
| 4 |
| a |
解得:a=2,a=-3,
∵点P,Q在第一象限,
∴a=2,

∴PQ=4,
又∵AD=3
∴S△APQ=
| 1 |
| 2 |
(3)∵D(a,0),l∥y轴,
∴P(a,2a+2),Q(a,
| 4 |
| a |
过C作CH⊥PQ于H,
∵C(1,4),
∴H(a,4),
∵PC=CQ,
∴PH=HQ,
∴2a+2-4=4-
| 4 |
| a |
解得:a=2,a=1(不合题意,舍去),
∴a=2.
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
模具英语词汇“上L曲、下L曲、上斜曲、下斜曲、上45°曲、顺送模具、轴垂检测机、圆跳动度检测机、多 2020-05-17 …
若曲线y=f(x)=x³-3ax²-3a²+a (a大于0)上有两点A(m,f(m)) B(n,f 2020-05-17 …
sinA=√5/5sin(A+B)=-√10/10A,B属于(0,π/2)求B若曲线y=f(x)= 2020-05-20 …
求在坐标N.M上的曲线N=M2+M+1和直线n=0.5.M=2,和M轴组成图形的面积 2020-05-23 …
曲轴上的平衡重一般设在( )。A.曲轴前端B.曲轴后端C.曲柄上D.曲柄销 2020-06-07 …
已知直线y=x上一点C(第三象限),过点C作CD⊥x轴于D,交双曲线y=k/x于点B过点C作CN⊥ 2020-06-12 …
已知M、N为双曲线y=4x(x>0)上的两点,且其横坐标分别为a、a+2,分别过M、N作y轴、x轴 2020-07-26 …
如图,直线y=2x+n与双曲线y=mx(m≠0)交于A,B两点,且点A的坐标为(1,4).(1)求m 2020-11-01 …
双曲线的实轴,虚轴分别在x轴,y轴上,双曲线线上一点P到两焦点F1,F2的距离分别为37/3和13/ 2020-11-13 …
如图1,直线Y=2X-4分别交X轴、Y轴于B、A两点.交双曲线Y=K/X(x>0)于点C,三角形AO 2021-01-10 …