如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=45．下列给出的结论中，正确的有（）①△ADE∽△ACD；②当BD=6时，△ABC与△DCE全等

Question

如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=

(4)/(5)．下列给出的结论中，正确的有（　　）
①△ADE∽△ACD；   
②当BD=6时，△ABC与△DCE全等；
③△DCE为直角三角形时，BD为8或12.5；
④0<CE≤6.4．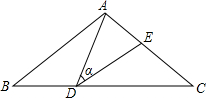

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

①∵AB=AC，
∴∠B=∠C，
又∵∠ADE=∠B
∴∠ADE=∠C，
∴△ADE∽△ACD；
故①正确，

②作AG⊥BC于G，
∵AB=AC=10，∠ADE=∠B=α，cosα=(4)/(5)，
∴BG=ABcosB，
∴BC=2BG=2ABcosB=2×10×(4)/(5)=16，
∵BD=6，
∴DC=10，
∴AB=DC，
在△ABD与△DCE中，

∠BAD=∠CDE

∠B=∠C

AB=DC

，
∴△ABD≌△DCE（ASA）．
故②正确，

③当∠AED=90°时，由①可知：△ADE∽△ACD，
∴∠ADC=∠AED，
∵∠AED=90°，
∴∠ADC=90°，
即AD⊥BC，
∵AB=AC，
∴BD=CD，
∴∠ADE=∠B=α且cosα=(4)/(5)，AB=10，
BD=8．
当∠CDE=90°时，易△CDE∽△BAD，
∵∠CDE=90°，
∴∠BAD=90°，
∵∠B=α且cosα=(4)/(5)．AB=10，
∴cosB=(AB)/(BD)=(4)/(5)，
∴BD=12.5．
故③正确．

④易证得△CDE∽△BAD，由②可知BC=16，
设BD=y，CE=x，
∴(AB)/(DC)=(BD)/(CE)，
∴(10)/(16-y)=(y)/(x)，
整理得：y²-16y+64=64-10x，
即（y-8）²=64-10x，
∴0<x≤6.4．
故④正确．
正确的有①②③④．
故选：D．