早教吧作业答案频道 -->数学-->
在平面直角坐标系中有一个正方形OACB，点A坐标为（4，0），M、N分别是OA、AC上的两个动点，当M点在OA上运动时，一直保持BM和MN垂直．（1）证明：Rt△BOM∽RtMAN；（2）设OM=x，梯形BOAN的面积
题目详情
在平面直角坐标系中有一个正方形OACB，点A坐标为（4，0），M、N分别是OA、AC上的两个动点，当M点在OA上运动时，一直保持BM和MN垂直．
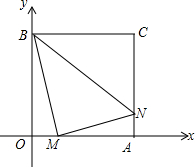
（1）证明：Rt△BOM∽RtMAN；
（2）设OM=x，梯形BOAN的面积为y，求y与x之间的函数关系式；
（3）当点M点运动到什么位置时S△BOM：SMAN=9：1，求x的值，并求出此时点N的坐标．
（1）证明：Rt△BOM∽RtMAN；
（2）设OM=x，梯形BOAN的面积为y，求y与x之间的函数关系式；
（3）当点M点运动到什么位置时S△BOM：SMAN=9：1，求x的值，并求出此时点N的坐标．
▼优质解答
答案和解析
（1）∵BM⊥MN，∴∠BMN=90°，即∠BMO+∠AMN=90°，∵∠BMO+∠OBM=90°，∴∠AMN=∠OBM，∵正方形OBCA中，∠BOM=∠MAN=90°，∴Rt△BOM∽Rt△MAN；（2）∵△BOM∽△MAN，∴BOMA=OMAN，∵A（4，0），正方形OBCA，∴O...
看了 在平面直角坐标系中有一个正方...的网友还看了以下：
已知圆x平方+y平方+x-6y+m=0和直线x+2y-3=0交于P,Q两点 且OP⊥OQ(O为坐已 2020-05-13 …
在平面直角坐标系中,O为坐标原点,A,B,C三点满足向量OC = 2/3 向量OA + 1/3在平 2020-05-16 …
在RT三角形ABC中O为AB上一点以OB为半径相切于D交AB与点E,AE=2,∠A=30度、一O为 2020-06-05 …
如图1，平面直角坐标系中，O为坐标原点，直线AB：y=12x+1分别交x、y轴于点A、B，过点A画 2020-06-14 …
在平面直角坐标系中,过A,O,C做圆O1,点E是劣弧AO上一点,连EC,EA,EO,当点E在劣弧A 2020-06-23 …
已知点A的坐标为（a，b），O为坐标原点，连接OA，将线段OA绕点O按逆时针方向旋转90°得OA1 2020-06-25 …
（）如图,在平面直角坐标系中,o是坐标原点,点A的坐标是（-4,0）,点C的坐标是（0,5）如图, 2020-07-30 …
数学题在平面直角坐标系中,O为坐标原点,已知向量a=(1,2),点A(1,0),B(cosX,T) 2020-08-01 …
如图，已知△OAB的顶点A（3，0），B（0，1），O是坐标原点．将△OAB绕点O按逆时针旋转90 2020-08-02 …
如图，在直角坐标系中，点O是坐标原点，四边形OABC是平行四边形，点A的坐标为（14，0），点B的 2020-08-03 …