早教吧作业答案频道 -->数学-->
△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为()A.3B.3C.5D.2+1
题目详情
△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )
A. 3
B. 3
C. 5
D.
+12
▼优质解答
答案和解析
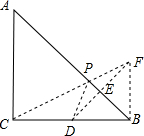 作D关于AB的对称点F,连接CF交AB于P,则CF的长度=PC+PD的最小值,连接PD,BF,
作D关于AB的对称点F,连接CF交AB于P,则CF的长度=PC+PD的最小值,连接PD,BF,
则AB垂直平分DF,
∴PF=PD,BD=BF=
BC=1,∠FBP=∠DBP,
∵△ABC为等腰直角三角形,AC=BC,
∴∠ACB=45°,
∴∠CBF=90°,
∴CF2=BC2+BF2=5,
∴CF=
,
∴PC+PD的最小值是
.
故选C.
 作D关于AB的对称点F,连接CF交AB于P,则CF的长度=PC+PD的最小值,连接PD,BF,
作D关于AB的对称点F,连接CF交AB于P,则CF的长度=PC+PD的最小值,连接PD,BF,则AB垂直平分DF,
∴PF=PD,BD=BF=
| 1 |
| 2 |
∵△ABC为等腰直角三角形,AC=BC,
∴∠ACB=45°,
∴∠CBF=90°,
∴CF2=BC2+BF2=5,
∴CF=
| 5 |
∴PC+PD的最小值是
| 5 |
故选C.
看了 △ABC为等腰直角三角形,∠...的网友还看了以下:
已知直线L:x=-1,点f(1,0)以F为焦点,L为相应的准线的椭圆(中心不在坐标原点)短轴的一顶 2020-05-16 …
(203秋•兴庆区校级月考)天体系统层示意图,图中为球所在的天系统P为某一天.成1-2题/格//A 2020-05-16 …
1.已知A,B是直线L同侧的两个定点,且到L得距离分别为a,b,P为L上的动点,则丨PA向量+3P 2020-05-16 …
如图,一次函数y=1/2x-2的图像分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位 2020-06-14 …
已知直线l:y=2x+m和椭圆C:x^/4+y^=1求以下问题1.当M为何值时,直线L被C截得的弦 2020-07-18 …
高二解析几何直线方程直线l过点P(2,-3),且与直线l1:x+3y-2=0相交与点A,与直线l2 2020-07-18 …
已知直线L:x=-1,点f(1,0)以F为焦点,L为相应的准线的椭圆(中心不在坐标原点)短轴的一顶 2020-07-31 …
已知椭圆x^2/a^2+y^2/b^2=1的左右两个焦点分别为F1F2,右顶点为A,上顶点为B,P 2020-07-31 …
已知平面直角坐标系中的点A,B的坐标分别为(3,0),(3,4),若以点A,B,P为与顶点的三角形与 2020-11-03 …
如图,四边形ABCD是正方形,E是CD上的一点,且CE比DE=1比3,P是BC上的点,如果△PCE与 2020-12-25 …