早教吧作业答案频道 -->数学-->
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.(1)若AC=4,BC=2,求OE的长.(2)试判断∠A与∠CDE的数量关系,并说明理由.
题目详情
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
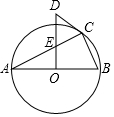
(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.

(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
▼优质解答
答案和解析
(1)∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,由勾股定理得:AB=
=
=2
,
∴OA=
AB=
,
∵OD⊥AB,
∴∠AOE=∠ACB=90°,
又∵∠A=∠A,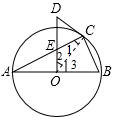
∴△AOE∽△ACB,
∴
=
,即
=
,
解得:OE=
;
(2)∠CDE=2∠A,理由如下:
连接OC,如图所示:
∵OA=OC,
∴∠1=∠A,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠2+∠CDE=90°,
∵OD⊥AB,
∴∠2+∠3=90°,
∴∠3=∠CDE,
∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.
∴∠ACB=90°,
在Rt△ABC中,由勾股定理得:AB=
| AC2+BC2 |
| 42+22 |
| 5 |
∴OA=
| 1 |
| 2 |
| 5 |
∵OD⊥AB,
∴∠AOE=∠ACB=90°,
又∵∠A=∠A,

∴△AOE∽△ACB,
∴
| OE |
| BC |
| OA |
| AC |
| OE |
| 2 |
| ||
| 4 |
解得:OE=
| ||
| 2 |
(2)∠CDE=2∠A,理由如下:
连接OC,如图所示:
∵OA=OC,
∴∠1=∠A,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠2+∠CDE=90°,
∵OD⊥AB,
∴∠2+∠3=90°,
∴∠3=∠CDE,
∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.
看了 如图,△ABC内接于⊙O,且...的网友还看了以下:
如图,在梯形ABCD中,AB‖CD,∠BAD=90°,以AD为直径的半圆O与BC相切.(2)若A 2020-05-01 …
如图,三角形ABC中角B=30度角C=60度AC=6,O为AB上一动点,以O为圆心,OA长为半径画 2020-05-16 …
已知,Rt△ABC中,∠C=90°,AC=4,BC=3.以AC上一点O为圆心的⊙O与BC相切于点C 2020-06-15 …
半圆O的圆心O在Rt△ABC的斜边AB上,且圆O分别切AC,BC于D,E两点,BC=a,AC=b, 2020-06-15 …
那位帮我啊...急..数学好的来(初三的)...Rt三角形ABC中,角C等于90度,o为斜边上一点 2020-07-19 …
如图,在△ABC中,∠C=90°,∠ACB的平分线交AB于点O,以O为圆心的⊙O与AC相切于点D. 2020-07-31 …
数学,紧急!1.已知△ABC的内切圆与边BC相切于点D,且点D恰为BC的中点,∠B=65°,求∠A 2020-07-31 …
(2013•永嘉县一模)如图,在△ABC中,∠C=90°,∠ACB的平分线交AB于点O,以O为圆心的 2020-12-22 …
∠MBC与∠NCBI的平分线交于点O,一O为圆心的○O与BC相切(1)求证○O与BM、CN相切(2) 2020-12-25 …
如图,∩MBC于∩NCB的平分线交于点O,以O为圆心的○o与bc相切.1.求证:○O与BM、CN相切 2020-12-25 …