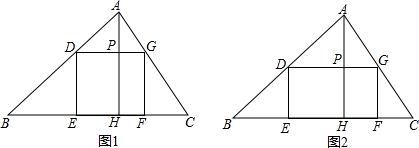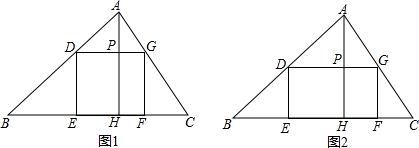如图,已知△ABC的边BC长15厘米,高AH为10厘米,四边形DEFG内接于△ABC,点E、F在边BC上,点D、G分别在边AB、AC上.(1)如图1,若四边形DEFG为正方形,求正方形的边长.(2)如图2,若四边形D
如图,已知△ABC的边BC长15厘米,高AH为10厘米,四边形DEFG内接于△ABC,点E、F在边BC上,点D、G分别在边AB、AC上.
(1)如图1,若四边形DEFG为正方形,求正方形的边长.
(2)如图2,若四边形DEFG为长方形,且DG:DE=2:1,则 的值为___.
答案和解析
(1)设DG为x,∵四边形DEFG是正方形,
∴DG∥BC,DG=DE=x,AP=10-x,
∴△ADG∽△ABC,
∴
=,
即=,
解得 x=6,
即DG=6;
(2)设DE为y,则DG=2y;,
∵四边形DEFG是长方形,
∴DG∥BC,AP=10-y,
∴△ADG∽△ABC,
∴=,
即=,解得y=,
∴2y=,
∵===,
∴=;
故答案为:.
如图中B、E为人体内两种重要有机物,G为某种细胞器.下列关于此图的叙述中,正确的是()A.e小分子 2020-05-13 …
已知A(g)+B(g)=C(g)△H=△H1D(g)+B(g)=E(g)△H=△H2,若A和D混合 2020-05-20 …
如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以 2020-05-24 …
关于高中对数函数的有关问题设g(x)=e(x)(x≤0)=lnx(x>0)1.求g(g(-2))g 2020-06-03 …
化合物E(含两种元素)与NH3反应生成化合物G和H2,G的式量为81.G分子中含硼元素40%、氢元 2020-07-05 …
修青藏铁路要测A.B两地的高度差,因地形情况,不易测出,我们在AB两点间找到合适的四个点,D.E. 2020-07-06 …
修青藏铁路要测A.B两地的高度差,因地形情况,不易测出,我们在AB两点间找到合适的四个点,D.E. 2020-07-06 …
f(x),g(x),h(x)在[a,b]上连续,(a,b)上可导,求证存在一个e属于(a,b)使得 2020-07-16 …
(2005•常州)如图所示,为使滑动变阻器的滑片P向右移动时,通电螺线管对条形磁铁的斥力变大,则电源 2020-11-12 …
图中,A、B、C、D、E是常见单质,其中B、C、E为金属.G、H、I、F是B、C、D、E分别和A形成 2021-01-12 …