如图，一次函数y=-x+4的图象与反比例函数y=kx（k为常数，且k≠0）的图象交于A（1，a），B两点．（1）求反比例函数的表达式及点B的坐标；（2）结合图象直接写出不等式-x+4>kx的解集（2）

Question

如图，一次函数y=-x+4的图象与反比例函数y=(k)/(x)（k为常数，且k≠0）的图象交于A（1，a），B两点．

（1）求反比例函数的表达式及点B的坐标；
（2）结合图象直接写出不等式-x+4>(k)/(x)的解集
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．

Answer 1

（1）∵点A（1，a）是一次函数y=-x+4与反比例函数y=(k)/(x)（k为常数，且k≠0）的交点，
∴

a=-1+4

a=k

，
解得：a=k=3，
∴反比例函数的表达式y=(k)/(x)=(3)/(x)，
解

y=-x+4

y=(3)/(x)

得：A（1，3），B（3，1），
故反比例函数的表达式y=(k)/(x)=(3)/(x)（x≠0），B点坐标为（3，1）．
（2）有图象知，当1<x<3时，直线图象在曲线的上方，
故不等式-x+4>(k)/(x)的解集为{x|1<x<3}．
（3）找B点关于x轴的对称点C，连接AC交x轴于P点，如图

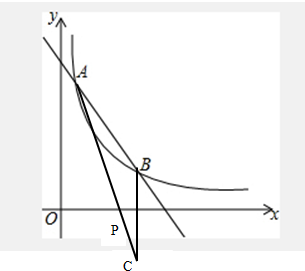
由（2）可知C点坐标为（3，-1），
∵PC=PB，PB，PC同线，所以此时PA=PB最短，
设直线AC方程为y=bx+c，
则有

3=b+c

-1=3b+c

，解得：b=-2，c=5，
故直线AC方程为y=-2x+5，将y=0代入其中得：x=2.5，
故得出P点坐标为（2.5，0），
又∵A（1，3），B（3，1），
∴△PAB的面积为(1)/(2)×（3+1）×（3-1）-(1)/(2)×（3-0）×（2.5-1）-(1)/(2)（1-0）（3-2.5）=1.5，
满足条件的P点坐标为（2.5，0），此时△PAB的面积面积为1.5．