早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=mx(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).(1)求反比例函数和一次函数的解析式;(2
题目详情
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=
(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).
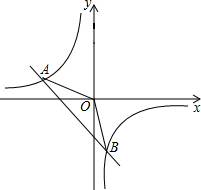
(1)求反比例函数和一次函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
| m |
| x |

(1)求反比例函数和一次函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
▼优质解答
答案和解析
(1)∵反比例函数y2=
(m为常数,且m≠0)的图象过点A(-2,1),
∴m=-2×1=-2,
∴反比例函数解析式为y2=-
;
∵点B(1,n)在反比例函数y2=-
的图象上,
∴n=-2,即点B(1,-2).
将点A(-2,1)、B(1,-2)代入到y1=ax+b(a,b为常数,且a≠0)中,
得:
,解得:
,
∴一次函数解析式为y1=-x-1.
(2)令y1=-x-1中x=0,则y=-1,
∴点C(0,-1),OC=1.
∴S△AOB=
OC•(xB-xA)=
×1×[1-(-2)]=
.
(3)观察函数图象,发现:
在x轴的下方,当x>1时,一次函数图象在反比例函数图形的下方,
∴当y1<y2<0时,自变量x的取值范围为x>1.
| m |
| x |
∴m=-2×1=-2,
∴反比例函数解析式为y2=-
| 2 |
| x |
∵点B(1,n)在反比例函数y2=-
| 2 |
| x |
∴n=-2,即点B(1,-2).
将点A(-2,1)、B(1,-2)代入到y1=ax+b(a,b为常数,且a≠0)中,

得:
|
|
∴一次函数解析式为y1=-x-1.
(2)令y1=-x-1中x=0,则y=-1,
∴点C(0,-1),OC=1.
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)观察函数图象,发现:
在x轴的下方,当x>1时,一次函数图象在反比例函数图形的下方,
∴当y1<y2<0时,自变量x的取值范围为x>1.
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
在一幅比例尺为1:500的平面图上量得一间长方形教室的周长是10厘米.长与宽的比是3:2.求教室的 2020-05-16 …
三棱台ABC-A`B`C`的上下底面均为正三角形,侧面为等腰梯形,且上下底面的边长比为2:3,分别 2020-05-21 …
为什么在用量筒量液体时,密度比水大的会成凹液面为什么在用量筒量液体时,密度比水小或等于水的会成凹液 2020-05-23 …
一个长方体的长、高、宽之比为4:3:2,其中长比高多6厘米,则这个长方体的棱长总和是?一个长方体的 2020-06-06 …
分子结构问题N2,N2+键长为109PM,112PM,Cl2,Cl2+键长为199PM和189PM 2020-07-18 …
丢硬币数学问题求解丢1000次硬币硬币有正反两面每一面概率都为50%求:(1)出现反面比正面(正面 2020-07-22 …
1.直角三角形的周长为2+根号7,斜边长为2,求这个直角三角形的面积.2.某村计划修建一条横断面为 2020-07-30 …
某林区2005年底的森林面积为m公顷,计划从2006年起,到2008年为止,每年年初砍伐一部分森林, 2020-11-08 …
在一幅比例尺为1:200的平面图上量得一间长方形教室的长是3cm,宽是2cm.1.求这间教室图上面积 2020-11-20 …
则水平比例尺应为若抛物线面上距离为2厘米,比例尺为一千万分之一,欲绘制该剖面线的剖面图,剖面图的基线 2020-12-05 …