我们把自变量为x的函数记为f（x），对于函数f（x）的自变量取值范围内的任意一个x、都有f（-x）=f（x），那么f（x）就叫做偶函数，对于函数f（x）的自变量取值范围内的任意一个x，都有f

Question

我们把自变量为x的函数记为f（x），对于函数f（x）的自变量取值范围内的任意一个x、都有f（-x）=f（x），那么f（x）就叫做偶函数，对于函数f（x）的自变量取值范围内的任意一个x，都有f（-x）=f（x），那么f（x）就叫做奇函数．
（1）对于反比例函数f（x）=(2)/(x)，判断它是奇函数还是偶函数，并说明理由
（2）已知函数f（x）=

x2-2x(x≥0)

ax2+bx+c(x<0)

是奇函数，求常数a，b，c的值
（3）已知直线y=x+m与（2）中函数图象恰好有一个交点，求常数m的范围．

Answer 1

（1）反比例函数f（x）=(2)/(x)是奇函数．理由如下：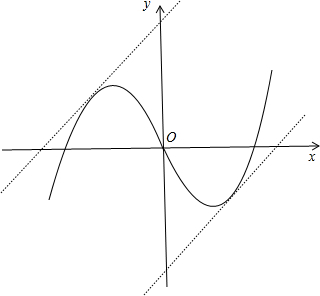
∵f（-x）=(2)/(-x)=-(2)/(x)=-f（x），
∴反比例函数f（x）=(2)/(x)是奇函数；
（2）∵x≥0时，f（x）=x²-2x，
而函数f（x）是奇函数，
∴f（-x）=-f（x）=-（x²-2x）=-x²+2x，
∵f（-x）=-（-x）²-2（-x），
∴当x<0时，f（x）=-x²-2x，
∴a=-1，b=-2，c=0；
（3）如图，当x≥0时，方程x²-2x=x+m有相等实数解，直线y=x+m与抛物线y=x²-2x（x≥0）只有一个公共点，即3²+4m=0，解得m=-(9)/(4)，所以当m<-(9)/(4)时，直线y=x+m与（2）中函数图象恰好有一个交点；
当x<0时，方程-x²-2x=x+m有相等实数解，直线y=x+m与抛物线y=-x²-2x（x<0）只有一个公共点，即3²-4m=0，解得m=(9)/(4)，所以当m>(9)/(4)时，直线y=x+m与（2）中函数图象恰好有一个交点，
综上所述，m的范围为m>(9)/(4)或m<-(9)/(4)．