早教吧作业答案频道 -->数学-->
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.(Ⅰ)求证:OM∥平面ABD;(Ⅱ)若AB=BC=2,求三棱锥A
题目详情
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
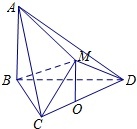
(Ⅰ)求证:OM∥平面ABD;
(Ⅱ)若AB=BC=2,求三棱锥A-BDM的体积.

(Ⅰ)求证:OM∥平面ABD;
(Ⅱ)若AB=BC=2,求三棱锥A-BDM的体积.
▼优质解答
答案和解析
(Ⅰ)证明:∵△CMD是等腰直角三角形,∠CMD=90°,点O为CD的中点,
∴OM⊥CD.
∵平面CMD⊥平面BCD,平面CMD∩平面BCD=CD,OM⊂平面CMD,
∴OM⊥平面BCD.
∵AB⊥平面BCD,
∴OM∥AB.
又∵AB⊂平面ABD,OM⊄平面ABD,
∴OM∥平面ABD.
(Ⅱ) 由(Ⅰ)知OM∥平面ABD,
∴点M到平面ABD的距离等于点O到平面ABD的距离.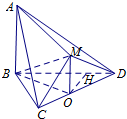
过O作OH⊥BD,垂足为点H,
∵AB⊥平面BCD,OH⊂平面BCD,
∴OH⊥AB.
∵AB⊂平面ABD,BD⊂平面ABD,AB∩BD=B,
∴OH⊥平面ABD.
∵AB=BC=2,△BCD是等边三角形,
∴BD=2,OD=1,OH=OD•sin60°=
.
∴VA-BDM=VM-ABD=VO-ABD=
×
×AB•BD•OH=
×
×2×2×
=
.
∴三棱锥A-BDM的体积为
.
∴OM⊥CD.
∵平面CMD⊥平面BCD,平面CMD∩平面BCD=CD,OM⊂平面CMD,
∴OM⊥平面BCD.
∵AB⊥平面BCD,
∴OM∥AB.
又∵AB⊂平面ABD,OM⊄平面ABD,
∴OM∥平面ABD.
(Ⅱ) 由(Ⅰ)知OM∥平面ABD,
∴点M到平面ABD的距离等于点O到平面ABD的距离.

过O作OH⊥BD,垂足为点H,
∵AB⊥平面BCD,OH⊂平面BCD,
∴OH⊥AB.
∵AB⊂平面ABD,BD⊂平面ABD,AB∩BD=B,
∴OH⊥平面ABD.
∵AB=BC=2,△BCD是等边三角形,
∴BD=2,OD=1,OH=OD•sin60°=
| ||
| 2 |
∴VA-BDM=VM-ABD=VO-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
∴三棱锥A-BDM的体积为
| ||
| 3 |
看了 如图,在多面体ABCDM中,...的网友还看了以下:
初中数学竞赛几何证明题已知点o为等边三角形ABC的内心,直线m过点o,过A、B、C三点分别作直线m 2020-05-16 …
直线m交x轴 y轴与点A B 与反比例函数的图像交于C D两点、直线m交x轴 y轴与点A B 与反 2020-05-16 …
若M={x|n=x/2,n∈Z},N={x|n=x+1/2,n∈Z},则M∩N等于A.空集B.{空 2020-05-20 …
如图,等腰三角形ABC的直角顶点C在直线m上,AD垂直于m,BE垂直于m,垂足分别为D,E.1.试 2020-06-04 …
练习:1.右图一中,P为直线m外一点,A,B,C为m上不同的三点且PB⊥m,那麼()(A)PA,P 2020-06-17 …
在△ABC和△DEF中,已知∠A=∠D=70°,∠B=50°,∠E=30°,画直线l,m,使直线l 2020-06-27 …
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, 2020-06-27 …
n在下m在上m//n,点B,C是直线n上两点,点A是直线m上一点(AB≠AC),在直线m上另找一点 2020-08-01 …
已知,在△ABC中,AB=AC,直线m经过点A,点D,E是直线m上的动点,且∠BDE=∠AEC=∠B 2020-11-03 …
(1).在三角形ABC中角BAC等于90度,AB等于AC,直线m经过A,BD垂直m,CE垂直m,垂足 2020-12-25 …