早教吧作业答案频道 -->数学-->
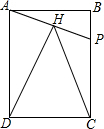
已知如图所示,矩形ABCD,P为BC上的一点,连接AP,过D点做DH⊥AP交AP与H,AB=22,BC=4,当△CDH为等腰三角形时,则BP=.
题目详情
已知如图所示,矩形ABCD,P为BC上的一点,连接AP,过D点做DH⊥AP交AP与H,AB=2
,BC=4,当△CDH为等腰三角形时,则BP=___.
| | 2 |

▼优质解答
答案和解析
过点H作HE⊥CD于点E,延长EH交AB于点F,连接DP,如图所示.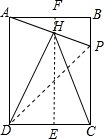
∵△CDH为等腰三角形,
∴点E为CD的中点,
∵EF∥AD,
∴FH为△ABP的中位线,
∴AH=HP.
∵DH⊥AP,
∴△DAP为等腰三角形,
∴AD=DP.
设BP=a,则CP=4-a,
由勾股定理得:DP2=CD2+CP2,即16=8+(4-a)2,
解得:a=4-2
,或a=-4-2
(舍去).
故答案为:4-2
.

∵△CDH为等腰三角形,
∴点E为CD的中点,
∵EF∥AD,
∴FH为△ABP的中位线,
∴AH=HP.
∵DH⊥AP,
∴△DAP为等腰三角形,
∴AD=DP.
设BP=a,则CP=4-a,
由勾股定理得:DP2=CD2+CP2,即16=8+(4-a)2,
解得:a=4-2
| 2 |
| 2 |
故答案为:4-2
| 2 |
看了 已知如图所示,矩形ABCD,...的网友还看了以下:
如图,等边△ABC中,AB=4,点P是AB边上的一个动点(点P可以与点A重合,但不与点B重合),过点 2020-03-31 …
概率基本公式歧义性,我用'符号表示非A,B为两个事件,求恰好有一个发生的概率.P(AB'∪A'B) 2020-05-13 …
概率论里面等式两边这么同时与一个事件还成立?即同时与一个A以后怎么成立如题AB=AB拔求P(AB) 2020-06-22 …
已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB 2020-07-22 …
一道数学题,看补充,若一点P把线段AB分成两段AP与BP(AP>BP),使AP的平方=PBXAB, 2020-07-24 …
如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一 2020-08-02 …
(2012•牡丹江)如图①,△ABC中.AB=AC,P为底边BC上一点,PE⊥AB,PF⊥AC,C 2020-08-03 …
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰 2020-11-04 …
概率论的问题.P(A)=0.6P(B)=0.7求P(AB)的最大值就是0.6但是下面的做法看起来对, 2020-11-28 …
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰 2020-12-31 …