22.已知数列{an}满足：a1=且an=(n≥2n∈N*).(1)求数列{an}的通项公式；(2)证明：对一切正整数n，不等式a1·a2·…·an＜2·n!恒成立.

Question

22.已知数列{a _n }满足：a ₁ = 且a _n = (n≥2 n∈N ^* ).

(1)求数列{a _n }的通项公式；

(2)证明：对一切正整数n，不等式a ₁ ·a ₂ ·…·a _n ＜2·n!恒成立.

Answer 1

(1)将条件变为：1- 因此，{1- }为一个等比数列，

其首项为1- 公比为 ，从而1- ，

据此得a _n = (n≥1)                            …………①

（2）证：据①得，a ₁ a ₂ …a _n = .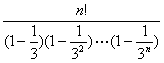

为证a ₁ a ₂ …a _n ＜2·n!，

只要证n∈N ^* 时有 ＞ .     …………②

显然，左端每个因式皆为正数，先证明，对每个n∈N*

≥1- .    …………③

用数学归纳法证明③式：

1°n=1时，显然③式成立，

2°设n=k时，③式成立

即 ≥1-

则当n=k+1时

≥［1- ］

=１- -

≥1- .

即当n=k+1时，③式也成立.

故对一切n∈N ^* ③式都成立.

利用③得， ≥1-

=1-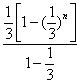

=1- ＞ .

故②式成立，从而结论得证.