（1）如图①，O的弦CE垂直于直径AB，垂足为点G，点D在CB上，作直线CD，ED，与直线AB分别交于点F，M，连接OC，求证：OC2=OM•OF；（2）把（1）中的“点D在CB上”改为“点D在AE上”，其余条件不

Question

（1）如图①， O的弦CE垂直于直径AB，垂足为点G，点D在

CB

上，作直线CD，ED，与直线AB分别交于点F，M，连接OC，求证：OC²=OM•OF；
（2）把（1）中的“点D在

CB

上”改为“点D在

AE

上”，其余条件不变（如图②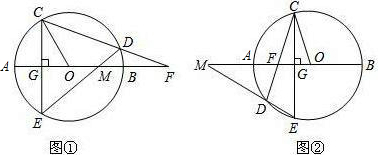），试问：（1）中的结论是否成立？并说明理由．

Answer 1

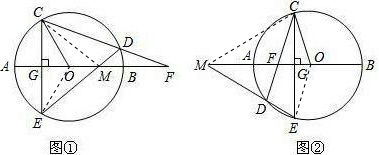（1）证明：如图①，连接CM，OE，
∵AB⊥CE于G，∴GC=GE．
∴MC=ME，∴∠CMA=∠EMA．
∠AOC=(1)/(2)∠COE，∴∠AOC=∠CDE．
又∠OCM=∠AOC-∠CMA，
∠F=∠CDE-∠DMF，
∠DMF=∠EMA，
∴∠OCM=∠F．
又∠COM=∠FOC，∴△OMC∽△OCF．
∴(OC)/(OF)=(OM)/(OC)．
∴OC²=OM•OF．

（2） 成立．理由如下：
如图②，连接MC，OE，
∵AB⊥CE于G，
∴GC=GE，

BC

=

BE

=(1)/(2)

CBE

．
∴∠CDE=∠COB，MC=ME．
∴∠EMG=∠CMO．
∵∠FCO=∠COB-∠OFC，∠EMG=∠CDE-∠DFM，∠DFM=∠OFC，
∴∠EMG=∠FCO．
∴∠FCO=∠CMO．
∴△OCF∽△OMC．
∴(OC)/(OM)=(OF)/(OC)，
∴OC²=OM•OF．