早教吧作业答案频道 -->数学-->
如图,点C是O上一点,O的半径为22,D、E分别是弦AC、BC上一动点,且OD=OE=2,则AB的最大值为()A.26B.23C.22D.42
题目详情
如图,点C是 O上一点, O的半径为2
,D、E分别是弦AC、BC上一动点,且OD=OE=2
,则AB的最大值为( )2 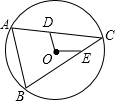
A. 26
B. 23
C. 22
D. 42
▼优质解答
答案和解析
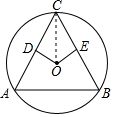 如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
连接OC,
∵ O的半径为2
,OD=
,
∴∠ACO=30°,
∴AC=2CD=2
=2
=2
,
同理可得∠BOC=30°,
∴∠ACB=60°,
∵OD=OE,OD⊥AC、OE⊥BC,
∴AC=BC,
∴△ABC是等边三角形,
∴AB=AC=2
,
即AB的最大值为2
.
故选A.
 如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,连接OC,
∵ O的半径为2
| 2 |
| 2 |
∴∠ACO=30°,
∴AC=2CD=2
| OC2-OD2 |
(2
|
| 6 |
同理可得∠BOC=30°,
∴∠ACB=60°,
∵OD=OE,OD⊥AC、OE⊥BC,
∴AC=BC,
∴△ABC是等边三角形,
∴AB=AC=2
| 6 |
即AB的最大值为2
| 6 |
故选A.
看了 如图,点C是O上一点,O的半...的网友还看了以下:
已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点E(0,-1)(1 2020-05-13 …
如图,点A(1,4)、B(2,a)在函数y=mx(x>0)的图象上,直线AB与x轴相交于点C,AD 2020-06-13 …
(2014•崇川区一模)如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC 2020-06-19 …
如图,点A、C为反比例函数y=kx(x<0)图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂 2020-07-24 …
如图,点A的坐标为(3,0),以点A为圆心,5个单位长度为半径画圆,分别交x轴于点B,C,交y轴于 2020-07-26 …
如图,点A(3,5)关于原点O的对称点为点C,分别过点A,C作y轴的平行线,与反比例函数y=kx( 2020-07-29 …
如图①,点A,E,F,C在一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD 2020-11-03 …
如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法 2020-11-06 …
(2014•武义县模拟)如图,点A是直线y=2x上一动点,以A为顶点的抛物线y=(x-m)2+h交直 2020-11-22 …
读图,完成下列问题:(1)根据经纬度描出下列各点:E(40°E,20°N)F(0°,20°N)G(3 2021-01-05 …