如图所示，水平面内的等边三角形ABC的边长为L，顶点C恰好位于光滑绝缘直轨道CD的最低点，光滑直导轨的上端点D到A、B两点的距离均为L，D在AB边上的竖直投影点为O．一对电荷量均为-Q的点

Question

如图所示，水平面内的等边三角形ABC的边长为L，顶点C恰好位于光滑绝缘直轨道CD的最低点，光滑直导轨的上端点D到A、B两点的距离均为L，D在AB边上的竖直投影点为O．一对电荷量均为-Q的点电荷分别固定于A、B两点．在D处将质量为m、电荷量为+q的小球套在轨道上（忽略它对原电场的影响），将小球由静止开始释放，已知静电力常量为k、重力加速度为g，且k

(Qq)/(L2)=(√(3))/(3)mg，忽略空气阻力，则（　　）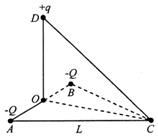

A. 轨道上D点的场强大小为

(mg)/(2q)

B. 小球刚到达C点时，其加速度为零

C. 小球刚到达C点时，其动能为

(√(3))/(2)mgL

D. 小球沿直轨道CD下滑过程中，其电势能先增大后减小

Answer 1

A、负电荷产生的电场指向负电荷，可知两个负电荷在D处的电场强度分别指向A与B，由于两个点电荷的电量是相等的，所以两个点电荷在D点的电场强度的大小相等，则它们的合场强的方向沿DA、DB的角平分线；
由库仑定律，A、B在D点的场强的大小：EA=EB=(kQ)/(L2)=(√(3)mg)/(3q)
它们的合场强：E_D=E_Acos30°+E_Bcos30°=(mg)/(q)．故A错误；
B、由几何关系宽度：

.

AO

=

.

CO

=(√(3))/(2)L，则：∠OCD=45°
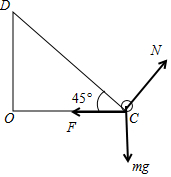对小球进行受力分析，其受力的剖面图如图：
由于C到A、B的距离与D到A、B的距离都等于L，结合A的分析可知，C点的电场强度的大小与D点的电场强度的大小相等，方向指向O点，即：EC=ED=(mg)/(q)
沿斜面方向：mgcos45°-F•cos45°=ma
垂直于方向：mgsin45°+Fsin45°=N
其中F是库仑力，F=q•EC=q•(mg)/(q)=mg
联立以上三式得：a=0．故B正确；
C、由于C与D到A、B的距离都等于L，结合等量同种点电荷的电场特点可知，C点与D点的电势是相等的，所以小球从D到C的过程中电场力做功的和等于0，则只有重力做功，小球的机械能守恒，得：mg•

.

OD

=(1)/(2)mv2
由几何关系可得：

.

OD

=L•sin60=(√(3)L)/(2)
小球的动能：Ek=(1)/(2)mv2=(√(3)mgL)/(2)，故C正确；
D、由几何关系可知，在CD的连线上，CD连线的中点处于到A、B的距离最小，电势最低，小球带正电，所以小球在CD的连线中点处的电势能最小．则小球沿直轨道CD下滑过程中，其电势能先减小后增大．故D错误．
故选：BC