如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，PN+PM+MN的最小值是5cm，则∠AOB的度数是．

Question

如图，点 P 是 ∠ AOB 内任意一点， OP=5cm ，点 M 和点 N 分别是射线 OA 和射线 OB 上的动点， PN+PM+MN 的最小值是 5cm ，则 ∠ AOB 的度数是 __________ ．

Answer 1

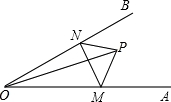
30 ° ．

【考点】轴对称 - 最短路线问题．

【分析】分别作点 P 关于 OA 、 OB 的对称点 C 、 D ，连接 CD ，分别交 OA 、 OB 于点 M 、 N ，连接 OC 、 OD 、 PM 、 PN 、 MN ，由对称的性质得出 PM=CM ， OP=OC ， ∠ COA= ∠ POA ； PN=DN ， OP=OD ， ∠ DOB= ∠ POB ，得出 ∠ AOB= ∠ COD ，证出 △ OCD 是等边三角形，得出 ∠ COD=60 ° ，即可得出结果．

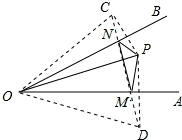
【解答】分别作点 P 关于 OA 、 OB 的对称点 C 、 D ，连接 CD ，

分别交 OA 、 OB 于点 M 、 N ，连接 OC 、 OD 、 PM 、 PN 、 MN ，如 图所示：

∵ 点 P 关于 OA 的对称点为 D ，关于 OB 的对称点为 C ，

∴ PM=DM ， OP=OD ， ∠ DOA= ∠ POA ；

∵ 点 P 关于 OB 的对称点为 C ，

∴ PN=CN ， OP=OC ， ∠ COB= ∠ POB ，

∴ OC=OP=OD ， ∠ AOB= ∠ COD ，

∵ PN+PM+MN 的最小值是 5cm ，

∴ PM+PN+MN=5 ，

∴ DM+CN+MN=5 ，

即 CD=5=OP ，

∴ OC=OD=CD ，

即 △ OCD 是等边三角形，

∴∠ COD=60 ° ，

∴∠ AOB=30 ° ．

故答案为： 30 ° ．

【点评】本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质；熟练掌握轴对称的性质， 证明三角形是等边三角形是解决问题的关键．