早教吧作业答案频道 -->数学-->
如图,点P是O外一点,PA切O于点A,AB是O的直径,连接OP,过点B作BC∥OP交O于点C,连接AC交OP于点D.(1)求证:PC是O的切线;(2)若PD=163,AC=8,求图中阴影部分的面积;(3)在(2)的条
题目详情
如图,点P是 O外一点,PA切 O于点A,AB是 O的直径,连接OP,过点B作BC∥OP交 O于点C,连接AC交OP于点D.
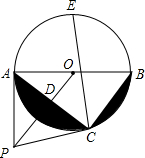
(1)求证:PC是 O的切线;
(2)若PD=
,AC=8,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是
的中点,连接CE,求CE的长.

(1)求证:PC是 O的切线;
(2)若PD=
| 16 |
| 3 |
(3)在(2)的条件下,若点E是
 |
| AB |
▼优质解答
答案和解析
(1)证明:如图1,连接OC,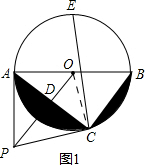
∵PA切 O于点A,∴∠PAO=90°,
∵BC∥OP,
∴∠AOP=∠OBC,∠COP=∠OCB,
∵OC=OB,∴∠OBC=∠OCB,
∴∠AOP=∠COP,
在△PAO和△PCO中,
,
∴△PAO≌△PCO,
∴∠PCO=∠PAO=90°,
∴PC是 O的切线;
(2) 由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90°,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD=∠AOD,
∴△ADP∽△ODA,
∴
=
,
∴AD2=PD•DO,
∵AC=8,PD=
,
∴AD=
AC=4,OD=3,AO=5,
由题意知OD为△的中位线,
∴BC=6,OD=6,AB=10.
∴S阴=
S O-S△ABC=
-24;
(3) 如图2,连接AE、BE,作BM⊥CE于M,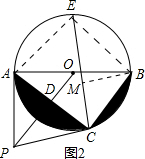
∴∠CMB=∠EMB=∠AEB=90°,
∵点E是
的中点,
∴∠ECB=∠CBM=∠ABE=45°,
CM=MB=3
,
BE=AB•cos45°=5
,
∴EM=
=4
,
则CE=CM+EM=7
.

∵PA切 O于点A,∴∠PAO=90°,
∵BC∥OP,
∴∠AOP=∠OBC,∠COP=∠OCB,
∵OC=OB,∴∠OBC=∠OCB,
∴∠AOP=∠COP,
在△PAO和△PCO中,
|
∴△PAO≌△PCO,
∴∠PCO=∠PAO=90°,
∴PC是 O的切线;
(2) 由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90°,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD=∠AOD,
∴△ADP∽△ODA,
∴
| AD |
| PD |
| DO |
| AD |
∴AD2=PD•DO,
∵AC=8,PD=
| 16 |
| 3 |
∴AD=
| 1 |
| 2 |
由题意知OD为△的中位线,
∴BC=6,OD=6,AB=10.
∴S阴=
| 1 |
| 2 |
| 25π |
| 2 |
(3) 如图2,连接AE、BE,作BM⊥CE于M,

∴∠CMB=∠EMB=∠AEB=90°,
∵点E是
 |
| AB |
∴∠ECB=∠CBM=∠ABE=45°,
CM=MB=3
| 2 |
BE=AB•cos45°=5
| 2 |
∴EM=
| BE2-BM2 |
| 2 |
则CE=CM+EM=7
| 2 |
看了 如图,点P是O外一点,PA切...的网友还看了以下:
尺规作图难题任意给出两条不平行的线段,在这两条线段内有一点P,怎样用尺规作图:使两条线段连接起来, 2020-04-26 …
如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两 2020-05-13 …
如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°P为底BC上一点(不 2020-05-13 …
已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外), 2020-06-23 …
在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:已知:直线l和 2020-06-30 …
数学证明题(圆)⊙O1和⊙2是等圆,P是O1O2的中点,过P作直线AD交⊙O1于A、B,交⊙O2于 2020-07-13 …
已知:直线ab及其上一点p.求作:直线mn,使得mn垂直ab于p 2020-07-19 …
(2010•铁岭)如图,已知△ABC中,AB=AC,∠A=36°.(1)尺规作图:在AC上求作一点 2020-07-24 …
过点P作圆O的切线PA,A为切线,过PA中点B作割线交圆O于C,D连接PC并延长交圆O于E,连接P 2020-07-31 …
如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是()①取 2020-11-06 …