早教吧作业答案频道 -->数学-->
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a-b+c>0,④4a+2b+c>0,⑤若点(-2,y1)和(-13,y2)在该图象上,则y1>y2,其中正确的结
题目详情
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a-b+c>0,④4a+2b+c>0,⑤若点(-2,y1)和(-
,y2)在该图象上,则y1>y2,其中正确的结论是___.(填入正确结论的序号)
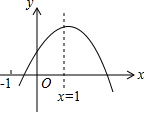
| 1 |
| 3 |
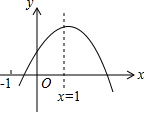
▼优质解答
答案和解析
∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∵对称轴x=-
>0,
∴b>0,
∴abc<0,故①正确;
∵对称轴x=-
=1,
∴b=-2a,
∴令x=-1时,此时y=a-b+c,
由图象可知a-b+c<0,
∴a+2a+c=3a+c<0,故②正确,③错误;
∵抛物线的对称轴为x=1,
∴-1与3关于x=1对称,0与2关于x=1对称,
令x=2时,此时y=4a+2b+c>0,故④正确;
当x<1时,y随着x的增大而增大,
∴-2<-
,
∴y1<y2,故⑤错误;
故答案为:②④
∴a<0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∵对称轴x=-
| b |
| 2a |
∴b>0,
∴abc<0,故①正确;
∵对称轴x=-
| b |
| 2a |
∴b=-2a,
∴令x=-1时,此时y=a-b+c,
由图象可知a-b+c<0,
∴a+2a+c=3a+c<0,故②正确,③错误;
∵抛物线的对称轴为x=1,
∴-1与3关于x=1对称,0与2关于x=1对称,
令x=2时,此时y=4a+2b+c>0,故④正确;
当x<1时,y随着x的增大而增大,
∴-2<-
| 1 |
| 3 |
∴y1<y2,故⑤错误;
故答案为:②④
看了 已知二次函数y=ax2+bx...的网友还看了以下:
函数的极值求详解,已知函数f(x)=x3+2x2+x-4,g(x)=ax2+x-8,求函数f(x) 2020-05-20 …
曲线f(x)=x3+ax2+bx+1的拐点个数是希望可以有具体的步骤, 2020-06-18 …
将一多项式(17x2-3x+4)-(ax2+bx+c),除以(5x+6)后,得商式为(2x+1), 2020-07-30 …
将一多项式(17x2-3x+4)-(ax2+bx+c),除以5x+6后,得商式为2x+1,余式为0 2020-07-30 …
求三次方程有三个正实数根的判别法.或者说,方程X3-aX2+bX-c=0,若a,b,c皆为正实数, 2020-07-31 …
关于x的二次三项式ax2+bx+c,满足下表中的对应关系:x…-5-4-2-101245…ax2+ 2020-07-31 …
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有 2020-08-01 …
一元二次方程都可以用ax2+bx+c=0表示那ax2+4=0少x和c呀 2020-08-03 …
抛物线y=ax2+bx+c开口向上向下分别说明什么还有ax2+bx+c=0大于0小于0的条件及原因 2020-12-15 …
(m2-1)x2-2mx-(m2-4)=0若ax2+bx+c=0(a不等于0,且a,b,c都是有理数 2021-02-02 …