早教吧作业答案频道 -->数学-->
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.(1)求抛物线对应的函数表达式;(2)判断△ABM的形状,并说明理由;(3)若将(1)
题目详情
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.
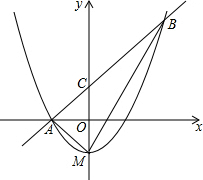
(1)求抛物线对应的函数表达式;
(2)判断△ABM的形状,并说明理由;
(3)若将(1)中的抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线过点(2,3)?

(1)求抛物线对应的函数表达式;
(2)判断△ABM的形状,并说明理由;
(3)若将(1)中的抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线过点(2,3)?
▼优质解答
答案和解析
(1)∵抛物线的顶点M在y轴上,
∴设抛物线的解析式为y=ax2+c,
当y=0时,有x+1=0,解得:x=-1,
∴A(-1,0);
当x=2时,y=2+1=3,
∴B(2,3).
将A(-1,0)、B(2,3)代入y=ax2+c中,
得:
,解得:
,
∴抛物线的解析式为y=x2-1.
(2)△ABM是直角三角形,理由如下:
当x=0,y=-1,
∴M(0,-1).
∵A(-1,0)、B(2,3),
∴AB=3
,AM=
,BM=2
,
∵AB2+AM2=20=BM2,
∴△ABM是直角三角形.
(3)由已知得:平移后的抛物线解析式为y=(x-m)2+2m,
∵点(2,3)在该抛物线上,
∴3=(2-m)2+2m,
解得:m=1.
∴设抛物线的解析式为y=ax2+c,
当y=0时,有x+1=0,解得:x=-1,
∴A(-1,0);
当x=2时,y=2+1=3,
∴B(2,3).
将A(-1,0)、B(2,3)代入y=ax2+c中,
得:
|
|
∴抛物线的解析式为y=x2-1.
(2)△ABM是直角三角形,理由如下:
当x=0,y=-1,
∴M(0,-1).
∵A(-1,0)、B(2,3),
∴AB=3
| 2 |
| 2 |
| 5 |
∵AB2+AM2=20=BM2,
∴△ABM是直角三角形.
(3)由已知得:平移后的抛物线解析式为y=(x-m)2+2m,
∵点(2,3)在该抛物线上,
∴3=(2-m)2+2m,
解得:m=1.
看了 如图,顶点M在y轴上的抛物线...的网友还看了以下:
一条抛物线的形状开口方向对称轴与抛物线y=1/2x^2相同,并且抛物线相同并且过(1,1).说明与 2020-04-07 …
如图,抛物线y=ax²+bx+4的对称轴是直线x=3/2,与x轴交于C,并且点A的坐标为(-1,0 2020-05-15 …
如图,抛物线y=-1/2x²+5/2x-2与X轴相交于A,B,与y轴相交于点C,过点C作CD∥X轴 2020-06-06 …
如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴 2020-06-14 …
如图,已知抛物线m:y=ax2-6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n: 2020-07-25 …
(2014•宝鸡一模)如图所示,在水平放置的半径为R的圆柱体轴线的正上方的P点,将一个小球以水平速度 2020-11-13 …
已知:抛物线Y=x²+bx-3与x轴相交于A,B两点,与Y轴相交于点C,并且OA=OC(1)\x05 2020-11-27 …
已知抛物线抛物线y^2=8x的焦点为F,准线l与x轴的交点为R,点A是抛物线上的点,链接AF并延长交 2020-12-23 …
在平面直角坐标系中,抛物线y=x2+2x-3与x轴交于A、B两点,(点A在点B左侧).与y轴交于点C 2020-12-25 …
(2014•大连)如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y 2021-01-09 …