如图，已知抛物线m：y=ax2-6ax+c（a>0）的顶点A在x轴上，并过点B（0，1），直线n：y=-12x+72与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（-7，7）．（1）求抛物

Question

如图，已知抛物线m：y=ax²-6ax+c（a>0）的顶点A在x轴上，并过点B（0，1），直线n：y=-(1)/(2)x+(7)/(2)与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（-7，7）．

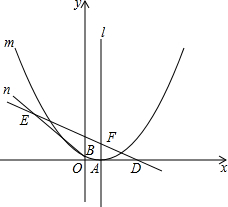
（1）求抛物线m的解析式；
（2）P是l上的一个动点，若以B，E，P为顶点的三角形的周长最小，求点P的坐标；
（3）抛物线m上是否存在一动点Q，使以线段FQ为直径的圆恰好经过点D？若存在，求点Q的坐标；若不存在，请说明理由．

Answer 1

（1）∵抛物线y=ax²-6ax+c（a>0）的顶点A在x轴上
∴配方得y=a（x-3）²-9a+1，则有-9a+1=0，解得a=(1)/(9)
∴A点坐标为（3，0），抛物线m的解析式为y=(1)/(9)x²-(2)/(3)x+1；
（2）∵点B关于对称轴直线x=3的对称点B′为（6，1）
∴连接EB′交l于点P，如图所示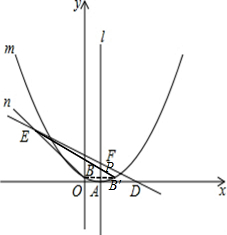
设直线EB′的解析式为y=kx+b，把（-7，7）（6，1）代入得

-7k+b=7

6k+b=1

  解得

k=-(6)/(13)

b=(49)/(13)

，
则函数解析式为y=-(6)/(13)x+(49)/(13)
把x=3代入解得y=(31)/(13)，
∴点P坐标为（3，(31)/(13)）；
（3）∵y=-(1)/(2)x+(7)/(2)与x轴交于点D，
∴点D坐标为（7，0），
∵y=-(1)/(2)x+(7)/(2)与抛物线m的对称轴l交于点F，
∴点F坐标为（3，2），
求得FD的直线解析式为y=-(1)/(2)x+(7)/(2)，若以FQ为直径的圆经过点D，可得∠FDQ=90°，则DQ的直线解析式的k值为2，
设DQ的直线解析式为y=2x+b，把（7，0）代入解得b=-14，则DQ的直线解析式为y=2x-14，
设点Q的坐标为（a，(1)/(9)a2-(2)/(3)a+1），把点Q代入y=2x-14得
(1)/(9)a2-(2)/(3)a+1=2a-14
解得a₁=9，a₂=15．
∴点Q坐标为（9，4）或（15，16）．