早教吧作业答案频道 -->数学-->
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.(1)求证:四边形EBFD是菱形;(2)已知AB=3,AD=9,求折痕EF的长.
题目详情
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.
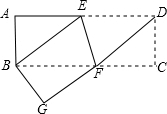
(1)求证:四边形EBFD是菱形;
(2)已知AB=3,AD=9,求折痕EF的长.

(1)求证:四边形EBFD是菱形;
(2)已知AB=3,AD=9,求折痕EF的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
由折叠的性质得:BE=DE,∠BEF=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF,
∴DE=BF,
∵DE∥BF,
∴四边形EBFD是平行四边形,
又∵BE=DE,
∴四边形EBFD是菱形;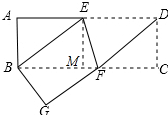
(2) 由(1)得:四边形EBFD是菱形,
∴BF=BE,
设BE=x,则BF=DE=BE=x,AE=AD-DE=9-x
在Rt△ABE中,AB2+AE2=BE2,
则32+(9-x)2=x2,
解得:x=5.
∴BF=BE=5,AE=4,
作EM⊥BC于M,
如图所示,则EM=AB=3,BM=AE=4,
∴MF=BF-BM=1,
∴EF=
=
=
.
∴AD∥BC,
∴∠DEF=∠BFE,
由折叠的性质得:BE=DE,∠BEF=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF,
∴DE=BF,
∵DE∥BF,
∴四边形EBFD是平行四边形,
又∵BE=DE,
∴四边形EBFD是菱形;

(2) 由(1)得:四边形EBFD是菱形,
∴BF=BE,
设BE=x,则BF=DE=BE=x,AE=AD-DE=9-x
在Rt△ABE中,AB2+AE2=BE2,
则32+(9-x)2=x2,
解得:x=5.
∴BF=BE=5,AE=4,
作EM⊥BC于M,
如图所示,则EM=AB=3,BM=AE=4,
∴MF=BF-BM=1,
∴EF=
| EM2+MF2 |
| 32+12 |
| 10 |
看了 如图,将矩形纸片ABCD沿E...的网友还看了以下:
如图,按要求画图(在相应图形中涂色)(1)将图形A平移到图形B;(2)将图形B沿图中虚线翻折到图形 2020-04-26 …
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图①);再沿过点E 2020-05-17 …
一张矩形纸片按如图所示的方法对折(先从下往上对折,再从左往右对折),然后沿着图中的虚线剪下,得到① 2020-05-21 …
一张矩形纸片按如图所示的方法对折(先从下往上对折,再从左往右对折),然后沿着图中的虚线剪下,得到① 2020-05-21 …
矩形ABCD中,AB=8,AD=6,将其沿锅过BD中点o的直线EF对折使B与D点重合,求折痕EF的 2020-06-06 …
(2013•江阴市一模)已知直线y=−34x+m与x轴y轴分别交于点A和点B,点B的坐标为(0,6 2020-07-15 …
如图①,在△ABC中,AB=AC,BC=acm,∠B=30°.动点P以1cm/s的速度从点B出发, 2020-07-20 …
如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP 2020-11-04 …
(2013•桐乡市一模)如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P 2020-11-04 …
如图1,将三角形纸片ABC沿折痕AD折叠,使得点C落在AB边的点G上,展开纸片沿折痕EF再次折叠,使 2021-01-22 …