早教吧作业答案频道 -->数学-->
已知平行四边形ABCD中,(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;(3)如图2,在(1)的基础上,连接B
题目详情
已知平行四边形ABCD中,
(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;
(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;
(3)如图2,在(1)的基础上,连接BE,DF,分别交FC,EA于点G,H.求证:四边形EHFG为平行四边形.
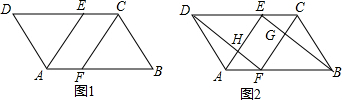
(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;
(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;
(3)如图2,在(1)的基础上,连接BE,DF,分别交FC,EA于点G,H.求证:四边形EHFG为平行四边形.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD.AB∥CD,
又∵DE=BF,
∴AB-BF=CD-DE.即AF=CE,
∴四边形AFCE是平行四边形.
(2)证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,AB∥CD,
∴∠BAE=∠DEA,
∵AE、CF分别是∠DAB,∠BCD的平分线,
∴∠BAE=∠DCF,
∴∠DEA=∠DCF,
∴AE∥CF,
∴四边形AFCE是平行四边形.
(3)证明:由(1)得:四边形AFCE是平行四边形,
∴AF=CE,AE∥CF,
∵AB=CD,
∴BF=DE,
又∵AB∥CD,
∴四边形BEDF为平行四边形,
∴DF∥BE,
∴四边形EHFG为平行四边形.
∴AB=CD.AB∥CD,
又∵DE=BF,
∴AB-BF=CD-DE.即AF=CE,
∴四边形AFCE是平行四边形.
(2)证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,AB∥CD,
∴∠BAE=∠DEA,
∵AE、CF分别是∠DAB,∠BCD的平分线,
∴∠BAE=∠DCF,
∴∠DEA=∠DCF,
∴AE∥CF,
∴四边形AFCE是平行四边形.
(3)证明:由(1)得:四边形AFCE是平行四边形,
∴AF=CE,AE∥CF,
∵AB=CD,
∴BF=DE,
又∵AB∥CD,
∴四边形BEDF为平行四边形,
∴DF∥BE,
∴四边形EHFG为平行四边形.
看了 已知平行四边形ABCD中,(...的网友还看了以下:
设A为实对称矩阵,求证若A^2=0,则A=0江湖救急! 2020-05-16 …
已知函数f(x)在区间(-∝,+∝)上是增函数,a,b∈R求证:若a+b≥0.则f(a)+f(b) 2020-05-17 …
求证一道初等矩阵题设A=(aij)m×n,B=(bij)n×p,且AB=0.试证若A的n个列向量线 2020-05-22 …
药品的鉴别是证明( )A.已知药物的真伪B.未知药物的真伪C.已知药物的疗效D.药物的稳定性E药物的 2020-06-07 …
已知a,b为正数,求证)若√a+1>√b,则对于任何大于1的正数x,恒有ax+x/(x-1)>b( 2020-06-12 …
几道关于整除的题目(很急啊,好的追分)1.求证:若3整除4X-Y,则9整除4倍的X平方+7XY-2 2020-06-30 …
1不属于S,若a属于S则1/(1-a)属于S,求证若a属于S1-1/a属于S这题意思是a=1/(1 2020-07-14 …
基本不等式的求证若a,b,c是实数,求证a立方+b立方+c立方>=3abc(>=为大于等于的意思) 2020-07-21 …
设A为实数集,满足a∈A==》1/1-a∈A,且1不属于A(1)若2∈A,求A(2)A能否为单元素 2020-07-30 …
若矩阵a与b可乘,试证若a有零行,则ab也有零行 2020-11-03 …