早教吧作业答案频道 -->数学-->
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,PF=3FB.(1)证明:EF∥平面ABC;(2)若∠BAC=60°,求点P到平面BCD的距离.
题目详情
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,
=3
.
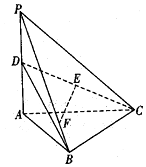
(1)证明:EF∥平面ABC;
(2)若∠BAC=60°,求点P到平面BCD的距离.
| PF |
| FB |

(1)证明:EF∥平面ABC;
(2)若∠BAC=60°,求点P到平面BCD的距离.
▼优质解答
答案和解析
(本小题满分12分)
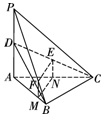
(Ⅰ)证明:法一:如图,过点F作FM∥PA交AB于点M,
取AC的中点N,连接MN,EN.
∵点E为CD的中点,∴EN
AD.又PF=3FB,∴MF
AD,∴FM
EN,
所以四边形MFEN为平行四边形,
∴EF∥MN,∵EF⊄平面ABC,MN⊂平面ABC,
∴EF∥平面ABC.…(6分)
法二:如图,取AD中点G,连接GE,GF,则GE∥AC,GF∥AB,
因为GE∩GF=G,AC∩AB=A,所以平面GEF∥平面ABC,
所以EF∥平面ABC.…(6分)
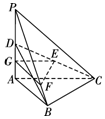
(Ⅱ) ∵PA⊥平面ABC,∴PA⊥BC.
又BC⊥AB,AB∩PA=A,
∴BC⊥平面PAB.
又∠BAC=60°,AC=2,∴AB=1, BC=
, BD=
,
∴S△BCD=
BC • BD=
.
记点P到平面BCD的距离为d,则VP-BCD=VC-PBD,∴
S△BCD • d=
S△PBD • BC,
∴
• d=
PD • AB • BC⇒d=
,
所以,点P到平面BCD的距离为d=
. …(12分)
(Ⅰ)证明:法一:如图,过点F作FM∥PA交AB于点M,
取AC的中点N,连接MN,EN.
∵点E为CD的中点,∴EN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
所以四边形MFEN为平行四边形,
∴EF∥MN,∵EF⊄平面ABC,MN⊂平面ABC,
∴EF∥平面ABC.…(6分)

法二:如图,取AD中点G,连接GE,GF,则GE∥AC,GF∥AB,
因为GE∩GF=G,AC∩AB=A,所以平面GEF∥平面ABC,
所以EF∥平面ABC.…(6分)

(Ⅱ) ∵PA⊥平面ABC,∴PA⊥BC.
又BC⊥AB,AB∩PA=A,
∴BC⊥平面PAB.
又∠BAC=60°,AC=2,∴AB=1, BC=
| 3 |
| 2 |
∴S△BCD=
| 1 |
| 2 |
| ||
| 2 |
记点P到平面BCD的距离为d,则VP-BCD=VC-PBD,∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以,点P到平面BCD的距离为d=
| ||
| 2 |
看了 如图,三棱锥P-ABC中,P...的网友还看了以下:
高数拉格朗日乘数法求极值(n元2个约束条件)的证明TT求F(x1,.,xn)驻点约束条件:G1(x 2020-04-25 …
已知函数f(x)定义在R上,对∀x,y∈R,有f(x+y)+f(x-y)=2f(x)•f(y),且 2020-05-13 …
设三角形ADE内接于圆O,弦BC分别交AD,AE边于F,G且弧AB等于弧AC.求证:F,D,E,G 2020-05-16 …
一道数学证明题f(0)=0,f'(0)>0,f''(x)0,求证f(x)在x>0上有零点感谢晶石同 2020-05-17 …
设函数f(x)二次可微分,且f''(x)>0,f(0)=0证明:函数F(x)=f(x)/x,x≠0 2020-06-08 …
f(x)在[0,1]连续,在(0,1)可导.f(0)=0,f(1)=1.证明存在两点a,b属于(f 2020-06-18 …
一道奇怪的数学证明题:设定义在R上的连续函数f(x)满足f'(x)=f(x)且有f(0)=0,证一 2020-06-22 …
设f(x)在闭区间[0,1]连续,在(0,1)内可导且f(0)=0,f(1)=1/3求证:彐ξ设f 2020-06-23 …
证明题(本大题5分)1.设f(x)在[0,1]上连续,且f(0)=0,f(1)=1.证明:至少存在 2020-08-01 …
求助一道数学题~设f(x)在〔0,1〕上连续,在(0,1)内可导,且f(0)=0,f(1)=1,a、 2020-12-28 …