早教吧作业答案频道 -->数学-->
如图,已知直线y=ax+b与双曲线y=kx(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C(1)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点
题目详情
如图,已知直线y=ax+b与双曲线y=
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C
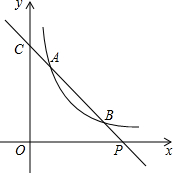
(1)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(2)探究证明x1,x2,x0之间的关系.
| k |
| x |

(1)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(2)探究证明x1,x2,x0之间的关系.
▼优质解答
答案和解析
(1)过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,如图所示.
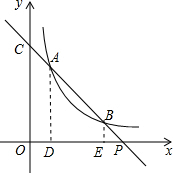
∵AD⊥x轴,BE⊥x轴,
∴BE∥AD∥y轴.
∵AB=BP,
∴DE=EP,
∴DP=DE+EP=2EP,AD=2BE,
∴y1=2y2.
∵x1y1=x2y2=k,即2x1y2=x2y2,
∴x2=2x1,
∴OE=2OD,
∴OD=DE=EP.
又∵点P的坐标为(6,0),
∴OP=6,x1=
OP=2,x2=
OP=4.
∵AD∥y轴,
∴△PAD∽△PCO,
∴
=
=
,
又∵b=y1+1,
∴点C的坐标为(0,y1+1),
∴
=
,
解得:y1=2.
∴y2=1.
故点A的坐标为(2,2),点B的坐标为(4,1).
(2)x0=x1+x2.
证明:∵点A、B在反比例函数图象上,
∴y1=
,y2=
,
∵BE∥AD,
∴△PBE∽△PAD,
∴
=
,即
=
,
∴x0=x1+x2.

∵AD⊥x轴,BE⊥x轴,
∴BE∥AD∥y轴.
∵AB=BP,
∴DE=EP,
∴DP=DE+EP=2EP,AD=2BE,
∴y1=2y2.
∵x1y1=x2y2=k,即2x1y2=x2y2,
∴x2=2x1,
∴OE=2OD,
∴OD=DE=EP.
又∵点P的坐标为(6,0),
∴OP=6,x1=
| 1 |
| 3 |
| 2 |
| 3 |
∵AD∥y轴,
∴△PAD∽△PCO,
∴
| OC |
| AD |
| OP |
| DP |
| 3 |
| 2 |
又∵b=y1+1,
∴点C的坐标为(0,y1+1),
∴
| OC |
| AD |
| y1+1 |
| y1 |
解得:y1=2.
∴y2=1.
故点A的坐标为(2,2),点B的坐标为(4,1).
(2)x0=x1+x2.
证明:∵点A、B在反比例函数图象上,
∴y1=
| k |
| x1 |
| k |
| x2 |
∵BE∥AD,
∴△PBE∽△PAD,
∴
| PE |
| PD |
| BE |
| AD |
| x0-x2 |
| x0-x1 |
| y2 |
| y1 |
∴x0=x1+x2.
看了 如图,已知直线y=ax+b与...的网友还看了以下:
两个最简二次根式3x2-6x+2与x2+x-1的被开方数相同,求x的值. 2020-05-14 …
若直线m被两平行线l1:x-y+1=0与x2:x-y+3=0所截得的线段的长为2倍根号2,则m的倾 2020-05-17 …
1.设X∈R,试比较X3与X2-X+1的大小(写出比较过程)我的解法如下:当X≥1时,X(X2+1 2020-06-18 …
已知x∈R,比较x2+1与x2+x的大小过程详细点拜托 2020-06-18 …
已知x>1,试比较x3-1与x2-x大小求 2020-06-18 …
设X≥1,比较因为比较x3与x2-x+1的大小解x-(x-x+1)=x-x+x-1=x(x-1)+ 2020-06-18 …
x2-x+1与x3比大小当x大或等于1…x3与x2-x+1比打小 2020-06-18 …
已知m为非负整数,当m取什么值时,关于x的方程x2+mx-1=0与x2+x+m-2=0仅有一个相同 2020-07-20 …
已知m为非负实数,当m取什么值时,关于x的方程x2+mx-1=0与x2+x+m-2=0仅有一个相同根 2020-11-08 …
若两个关于x的整式x2+(a+b)x+5b与x2-x-30恒等,则a=,b=. 2020-12-22 …