早教吧作业答案频道 -->数学-->
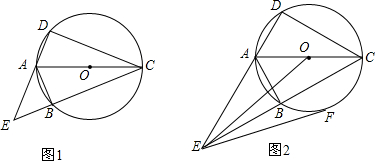
已知四边形ABCD内接于O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30
题目详情
已知四边形ABCD内接于 O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与 O的位置关系,并说明理由.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与 O的位置关系,并说明理由.

▼优质解答
答案和解析
 (1)证明:∵对角线AC平分∠DCB,
(1)证明:∵对角线AC平分∠DCB,
∴∠ACD=∠ACB,
∴
=
,
∴AD=AB,
∵EB=AD,
∴AB=EB,
∵∠EBA=∠ADC=90°,
∴△ABE是等腰直角三角形
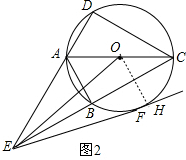
(2) 直线EF与 O相离.理由如下:
∵∠DCB<90°,∠ACD=∠ACB,
∵∠ACE≥30°,
∴60°≤∠DCE<90°,
∴∠AEC≤30°,
∴AE≥AC,
∵OE>AE,
∴OE>AC,
作OH⊥EF于H,如图,
在Rt△OEH中,∵∠OEF=30°,
∴OH=
OE,
∴OH>OA,
∴直线EF与 O相离.
 (1)证明:∵对角线AC平分∠DCB,
(1)证明:∵对角线AC平分∠DCB,∴∠ACD=∠ACB,
∴
 |
| AD |
 |
| AB |
∴AD=AB,
∵EB=AD,
∴AB=EB,
∵∠EBA=∠ADC=90°,
∴△ABE是等腰直角三角形
(2) 直线EF与 O相离.理由如下:
∵∠DCB<90°,∠ACD=∠ACB,
∵∠ACE≥30°,
∴60°≤∠DCE<90°,
∴∠AEC≤30°,
∴AE≥AC,
∵OE>AE,
∴OE>AC,
作OH⊥EF于H,如图,
在Rt△OEH中,∵∠OEF=30°,
∴OH=
| 1 |
| 2 |
∴OH>OA,
∴直线EF与 O相离.
看了 已知四边形ABCD内接于O,...的网友还看了以下:
如图,在rt三角形abc中,角bdc等于30度,延长cd到点a使ad等于db,连接ab,角a等于5 2020-04-09 …
急求如图,△ABC中,∠ABC=90°,E为AC的中点.在图中作点D,使AD‖BE,且∠ADC=9 2020-06-15 …
如图,在Rt三角形BCD中,延长CD到点A,使AD等于DB,连接AB,角A等于15度,求tan15 2020-07-09 …
如图,在rt△中,∠d=30度,延长cd到点a,使ad=db.连接ab,∠a=15°,求tan15 2020-07-09 …
已知,如图,AD、A'D'分别为锐角三角形ABC和锐角三角形A'B'C'的边BC和B'C'上的高, 2020-07-19 …
如图.圆0为三角形ABc的外接圆.Bc为圆0的直径,作射线BF,使BA平分角cBF.过点A作AD垂 2020-07-30 …
八年级全等三角形的问题?已知三角形ABC全等于三角形DEF,若三角形ABC的周长为22,AB等于8 2020-08-01 …
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′ 2020-11-03 …
在x轴上找一点E,y轴上找一点D,使AD+DE+BE的值为最小,求最小值在x轴上找一点C,使ABC周 2020-11-08 …
有一张矩形纸片ABCD,AB=根号3,AD=根号2,将纸片折叠,使点D落在AB边上的点D'处,折痕为 2020-12-21 …