早教吧作业答案频道 -->数学-->
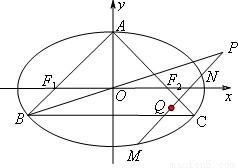
已知椭圆E:的离心率为,它的上顶点为A,左、右焦点分别为F1,F2,直线AF1,AF2分别交椭圆于点B,C.(1)求证直线BO平分线段AC;(2)设点P(m,n)(m,n为常数)在直线BO上
题目详情
已知椭圆E: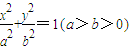 的离心率为
的离心率为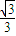 ,它的上顶点为A,左、右焦点分别为F 1 ,F 2 ,直线AF 1 ,AF 2 分别交椭圆于点B,C.
,它的上顶点为A,左、右焦点分别为F 1 ,F 2 ,直线AF 1 ,AF 2 分别交椭圆于点B,C.
(1)求证直线BO平分线段AC;
(2)设点P(m,n)(m,n为常数)在直线BO上且在椭圆外,过P的动直线l与椭圆交于两个不同点M,N,在线段MN上取点Q,满足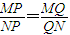 ,试证明点Q恒在一定直线上.
,试证明点Q恒在一定直线上.
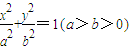 的离心率为
的离心率为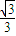 ,它的上顶点为A,左、右焦点分别为F 1 ,F 2 ,直线AF 1 ,AF 2 分别交椭圆于点B,C.
,它的上顶点为A,左、右焦点分别为F 1 ,F 2 ,直线AF 1 ,AF 2 分别交椭圆于点B,C.(1)求证直线BO平分线段AC;
(2)设点P(m,n)(m,n为常数)在直线BO上且在椭圆外,过P的动直线l与椭圆交于两个不同点M,N,在线段MN上取点Q,满足
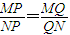 ,试证明点Q恒在一定直线上.
,试证明点Q恒在一定直线上.
▼优质解答
答案和解析
分析:
(1)利用离心率计算公式,及b2=a2-c2=2c2,可以用c表示a,b,即可表示椭圆的标准方程,进而得到点A,F1的坐标;与椭圆的方程联立即可解得点B的坐标,利用对称性即可得到点C的坐标,利用中点坐标公式即可得到相等AC的中点坐标,满足直线BO的方程即可;(2)设过P的直线l与椭圆交于两个不同点的坐标为M(x1,y1),N(x2,y2),点Q(x,y),可得,.设=λ,则,,利用向量相等即可得到m,n,x,y用x1,y1,x2,y2,λ表示,进而得到2mx+3ny为常数即可.
证明:(1)由题意,,则,b2=a2-c2=2c2,故椭圆方程为,即2x2+3y2-6c2=0,其中,F1(-c,0),∴直线AF1的斜率为,此时直线AF1的方程为,联立得2x2+3cx=0,解得x1=0(舍)和,即B,由对称性知.直线BO的方程为,线段AC的中点坐标为,AC的中点坐标满足直线BO的方程,即直线BO平分线段AC.(2)设过P的直线l与椭圆交于两个不同点的坐标为M(x1,y1),N(x2,y2),点Q(x,y),则,.设=λ,则,,求得,,,,∴,,∴2mx+3ny====6c2,由于m,n,C为常数,所以点Q恒在直线2mx+3ny-6c2=0上.
点评:
本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量共线等基础知识与方法,需要较强的推理能力与计算能力.
分析:
(1)利用离心率计算公式,及b2=a2-c2=2c2,可以用c表示a,b,即可表示椭圆的标准方程,进而得到点A,F1的坐标;与椭圆的方程联立即可解得点B的坐标,利用对称性即可得到点C的坐标,利用中点坐标公式即可得到相等AC的中点坐标,满足直线BO的方程即可;(2)设过P的直线l与椭圆交于两个不同点的坐标为M(x1,y1),N(x2,y2),点Q(x,y),可得,.设=λ,则,,利用向量相等即可得到m,n,x,y用x1,y1,x2,y2,λ表示,进而得到2mx+3ny为常数即可.
证明:(1)由题意,,则,b2=a2-c2=2c2,故椭圆方程为,即2x2+3y2-6c2=0,其中,F1(-c,0),∴直线AF1的斜率为,此时直线AF1的方程为,联立得2x2+3cx=0,解得x1=0(舍)和,即B,由对称性知.直线BO的方程为,线段AC的中点坐标为,AC的中点坐标满足直线BO的方程,即直线BO平分线段AC.(2)设过P的直线l与椭圆交于两个不同点的坐标为M(x1,y1),N(x2,y2),点Q(x,y),则,.设=λ,则,,求得,,,,∴,,∴2mx+3ny====6c2,由于m,n,C为常数,所以点Q恒在直线2mx+3ny-6c2=0上.
点评:
本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量共线等基础知识与方法,需要较强的推理能力与计算能力.
看了 已知椭圆E:的离心率为,它的...的网友还看了以下:
(1)画出“弦图”,并利用“弦图”证明勾股定理.(2)如图,是4个完全相同的直角三角形适当拼接后形 2020-06-10 …
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC 2020-06-12 …
(2014•龙东地区)已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m 2020-06-15 …
完成下面的证明,用反证法证明“两条直线被第三条直线所截,如果同位角不相等,那么这两条直线不平行”. 2020-07-23 …
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点, 2020-07-30 …
用反证法证明:已知,在同一平面内有三条直线a,b,c,a⊥c,b⊥c.求证:a∥b.证明:假设所求 2020-08-01 …
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE, 2020-08-03 …
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位 2020-11-02 …
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC, 2020-11-26 …
几何课本第三册复习题七中有这样一道几何题:以Rt△ABC的直角边AC为直径作圆,交斜边AB于点D,过 2020-12-13 …