早教吧作业答案频道 -->数学-->
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.(1)求证:S△ADE=S△ABC;(2)求证:AG平分DE.
题目详情
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.
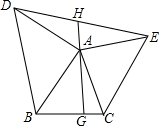
(1)求证:S△ADE=S△ABC;
(2)求证:AG平分DE.

(1)求证:S△ADE=S△ABC;
(2)求证:AG平分DE.
▼优质解答
答案和解析
(1)证明:作DP⊥GA,EQ⊥GA,垂足分别为P、Q.
∵Rt△ABD是等腰三角形,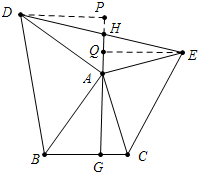
∴DA=BA,
∵∠PDA+∠PAD=90°,
∠PAD+∠BAG=90°,
∴∠PDA=∠BAG,
在△DAP与△ABG中,
,
∴△DAP≌△ABG(AAS),
∴DP=AG,
同理△AGC≌△EQA,AG=FQ.,
∴DP=EQ,
∴S△ABG=S△DAP,S△EQA=S△AGC,
在△DPH与△EQH中,
,
∴△DPH≌△EQH(AAS),
∴S△DPH=S△EQH,
∴S△ABC=S△ABG+S△AGC=S△DAP-S△DPH+S△EQA-S△EQH=S△DAP+S△EQA=S△ADE,
即S△ABC=S△ADE.
(2)证明:∵△DPH≌△EQH(已证),
∴DH=HE,
∴AG平分DE.
∵Rt△ABD是等腰三角形,

∴DA=BA,
∵∠PDA+∠PAD=90°,
∠PAD+∠BAG=90°,
∴∠PDA=∠BAG,
在△DAP与△ABG中,
|
∴△DAP≌△ABG(AAS),
∴DP=AG,
同理△AGC≌△EQA,AG=FQ.,
∴DP=EQ,
∴S△ABG=S△DAP,S△EQA=S△AGC,
在△DPH与△EQH中,
|
∴△DPH≌△EQH(AAS),
∴S△DPH=S△EQH,
∴S△ABC=S△ABG+S△AGC=S△DAP-S△DPH+S△EQA-S△EQH=S△DAP+S△EQA=S△ADE,
即S△ABC=S△ADE.
(2)证明:∵△DPH≌△EQH(已证),
∴DH=HE,
∴AG平分DE.
看了 如图,在△ABC中,以A为顶...的网友还看了以下:
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
35x+8是不是一个方程?再问多几个问题!(都是判断题,不用说原因)1、在“a除以b”中,a和b可 2020-05-21 …
为什么这样能画出角平分线,怎么说明设角ABC,以点A为顶点,圆规尖固定在A点,以任意半径画圆,分别 2020-06-04 …
设f(x)在x=a处连续,φ(x)在x=a处间断,又f(a)≠0,则()A.φ[f(x)]在x=a 2020-06-12 …
定积分证明题设f(x)在[-a,a]上连续,具有二阶连续导数,且f(0)=0证明:在[-a,a]上 2020-06-12 …
初三物理题歹徒在A处以5M/S速度逃跑.某地区道路如图所示(为一个RT△ABC,AB=40m,BC 2020-07-02 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
设f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是()A.limh→+ 2020-07-31 …
a,b为一面直线,则下列结论正确的是()A过不在a,b上的任一点,可做一个平面与a,b平行B过不在a 2020-12-23 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …