若k≠0,n是大于1的自然数,二项式(1+xk)n的展开式为a0+a1x+a2x2+a3x3+a4x4…+anxn.若点Ai(i,ai)(i=0,1,2)的位置如图所示,则∫k-1x2dx的值为()A.283B.263C.28D.26
若k≠0,n是大于1的自然数,二项式(1+
)n的展开式为a0+a1x+a2x2+a3x3+a4x4…+anxn.若点Ai(i,ai)(i=0,1,2)的位置如图所示,则x k
x2dx的值为( )∫ 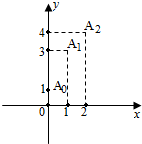
A. 28 3
B. 26 3
C. 28
D. 26
| x |
| k |
| C | r n |
| x |
| k |
| 1 |
| kr |
| C | r n |
由图可知,a0=1,a1=3,a2=4,
∴
| 1 |
| k |
| C | 1 n |
| 1 |
| k2 |
| C | 2 n |
∴
| n |
| k |
| n(n-1) |
| 2k2 |
∴k=3,
∴
| ∫ | k -1 |
| ∫ | 3 -1 |
| x3 |
| 3 |
| | | 3 -1 |
| 28 |
| 3 |
故选:A.
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
关于极限的题目a(n)=n*sin(∏/n)(n>=1)当n→∞时,求a(n)(n)为下标a(n) 2020-05-14 …
lim(a^n/n+b^n/n^2)^(1/n)(a>0,b>0)n->无穷()^(1/n)表示括 2020-06-23 …
一个畜水池有若干根管子,如果同时打开6根用5/2小时可以充满(池里原无水),如果同时用5根管子,用 2020-07-12 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
[√ā+1/a](n)展开式中无常数项,则n为()。A.任意正偶数B.不是3的倍数C.任意正奇数D 2020-07-31 …
基本不等式设数列a(n),b(n),且a(1)>b(1)>0,a(n)=(a(n-1)+b(n-1 2020-08-03 …
设数列{an}满足a(n+1)=2an+n^2-4n+1.(1)若a1=3,求证:存在f(n)=an 2020-11-19 …
一个求通项问题..a(n)=[a(n-1)]/[2a(n-1)+1]这个不是把分母乘过去,然后左右两 2020-12-14 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …