早教吧作业答案频道 -->数学-->
点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=;(2)如图②,将三角板MON绕点O逆
题目详情
点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=___;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=
∠AOM,求∠NOB的度数.
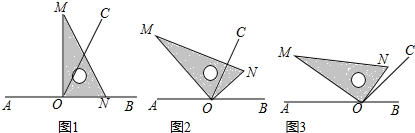
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=___;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=
| 1 |
| 4 |

▼优质解答
答案和解析
(1)∵∠MON=90°,∠BOC=65°,
∴∠MOC=∠MON-∠BOC=90°-65°=25°.
故答案为:25°.
(2)∵∠BOC=65°,OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB-∠MON
=130°-90°
=40°.
∠CON=∠COB-∠BON
=65°-40°
=25°.
(3)∵∠NOC
∠AOM,
∴∠AOM=4∠NOC.
∵∠BOC=65°,
∴∠AOC=∠AOB-∠BOC
=180°-65°
=115°.
∵∠MON=90°,
∴∠AOM+∠NOC=∠AOC-∠MON
=115°-90°
=25°.
∴4∠NOC+∠NOC=25°.
∴∠NOC=5°.
∴∠NOB=∠NOC+∠BOC=70°.
∴∠MOC=∠MON-∠BOC=90°-65°=25°.
故答案为:25°.
(2)∵∠BOC=65°,OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB-∠MON
=130°-90°
=40°.
∠CON=∠COB-∠BON
=65°-40°
=25°.
(3)∵∠NOC
| 1 |
| 4 |
∴∠AOM=4∠NOC.
∵∠BOC=65°,
∴∠AOC=∠AOB-∠BOC
=180°-65°
=115°.
∵∠MON=90°,
∴∠AOM+∠NOC=∠AOC-∠MON
=115°-90°
=25°.
∴4∠NOC+∠NOC=25°.
∴∠NOC=5°.
∴∠NOB=∠NOC+∠BOC=70°.
看了 点O为直线AB上一点,过点O...的网友还看了以下:
由三颗质量相等的恒星组成等边三角形,他们围绕三角形的中心匀速转动,他们之间的距离均为R,绕中心转动 2020-04-11 …
若5x2y|m|-(m+1)y2-3是三次三项式,则m等于( )如题:若5x2y|m|-4(1)( 2020-05-13 …
已知5x^2y^|m|-1/2(m-1)y^2+1是关于x,y的三次三项,求代数式m+1/m的值 2020-05-13 …
已知m平方-5m+1=0,求(1)m三次方+1/m三次方的值 (2)m-1/m的值 2020-05-16 …
设向量a,b是不共线的两个非零向量,向量OM=m向量a,向量ON=n向量b,向量OP=α向量aβ向 2020-06-06 …
如图,是两块完全一样的含角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设 2020-07-16 …
如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起 2020-07-22 …
若X²+X-3=0,求3-X²-X三次方/X-1的值已知关于X的方程X-1/X-3=M平方/2X- 2020-07-31 …
初三下册数学锐角三角函数的一道题,求详解已知a为锐角,m=sina+cosa,则m的取值范围.其实这 2020-12-08 …
已知:直角三角形ABC中,角C=90,AC=a,BC=b,将一块三角尺的直角顶点与斜边AB的中点M重 2021-01-22 …