早教吧作业答案频道 -->数学-->
如图1,定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形,如图2,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=12∠E.
题目详情
如图1,定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形,如图2,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=
∠E.
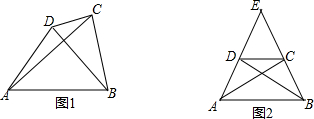
| 1 |
| 2 |
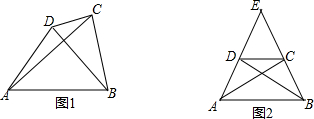
▼优质解答
答案和解析
证明:∵AE=BE,
∴∠EAB=∠EBA,
∵四边形ABCD是互补等对边四边形,
∴AD=BC,
在△ABD与△BAC中,
,
∴△ABD≌△BAC(SAS),
∴∠ABD=∠BAC,∠ADB=∠BCA,
∵∠ADB+∠BCA=180°,
∴∠ADB=∠BCA=90°,
在等腰△ABE中,∠EAB=∠EBA=(180°-∠E)÷2=90°-
∠E,
∴∠ABD=90°-∠EAB=90°-(90°-
∠E)=
∠E,
∴∠ABD=∠BAC=
∠E.
∴∠EAB=∠EBA,
∵四边形ABCD是互补等对边四边形,
∴AD=BC,
在△ABD与△BAC中,
|
∴△ABD≌△BAC(SAS),
∴∠ABD=∠BAC,∠ADB=∠BCA,
∵∠ADB+∠BCA=180°,
∴∠ADB=∠BCA=90°,
在等腰△ABE中,∠EAB=∠EBA=(180°-∠E)÷2=90°-
| 1 |
| 2 |
∴∠ABD=90°-∠EAB=90°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABD=∠BAC=
| 1 |
| 2 |
看了 如图1,定义:在四边形ABC...的网友还看了以下:
1.已知a,b,c是正有理数.求证:a^3/(a^2+ab+b^2)+b^3/(b^2+bc+c^ 2020-06-12 …
正确率要达到90%以上1.(-2)^101+(-2)^100=2.a^3·(-a^2)^3÷a^5 2020-07-22 …
aa(x-1)/(x-2)>2的解集为A,切3不属于A,求A和a的取值范围若a(x-1)/(x-2 2020-08-01 …
(2012•玉林)如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上, 2020-08-02 …
基本不等式的使用问题a+b=1,求(a+2)^2+(b+2)^2的最小值.在这道题里,如果使用基本 2020-08-03 …
a^3+a^3=(-a^2)^3=(-a^3)^2=(-x)^2×(-x)^5×(-x^4)=已知x 2020-11-01 …
(1)10^7除以(10^3除以10^2)(2)(x-y)^3*(x-y)^2*(y-x)(3)4* 2020-11-01 …
做出下面的题1.已知有理数a,b满足a^2+4b^2-a+4b+5/4=0;那么,-ab的相反数是多 2020-11-01 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …