早教吧作业答案频道 -->数学-->
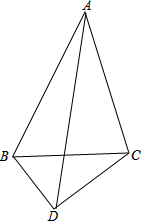
如图,∠BAC=45°,BD:DC:BC=3:4:5,AD=4,∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,求四边形ABCD的面积.
题目详情
如图,∠BAC=45°,BD:DC:BC=3:4:5,AD=4,∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,求四边形ABCD的面积.

▼优质解答
答案和解析
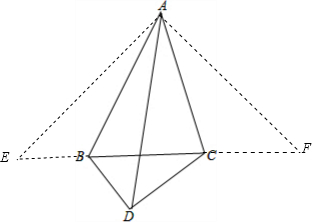 ∵BD:DC:BC=3:4:5,
∵BD:DC:BC=3:4:5,
∴设BD=3λ,则DC=4λ,BC=5λ;
如图,将△ABD、△ACD分别沿AB、AC折叠,得到△ABE和△ACF;
则∠ABE=∠ABD,∠ACD=∠ACF;
AE=AD=4,AF=AD=4;∠EAB=∠DAB,∠FAC=∠DAC;
∵∠BAC=45°,
∴∠EAF=90°
∵∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,
∴∠ABC+∠ABE=180°,∠ACB+∠ACF=180°,
∴E、B、C、F四点共线;
∵∠EAF=90°,
∴△EAF为等腰直角三角形,
∴△AEF的面积=
AE•AF=
×4×4=8;
∵(3λ)2+(4λ)2=(5λ)2,
∴△BDC为直角三角形;
EF=3λ+4λ+5λ=12λ;
由勾股定理得:(12λ)2=42+42,
解得:λ=
,BD=
,DC=
,
∴△BDC的面积=
×
×
=
;
设△ABD、△ADC、△BDC的面积分别为x,y,z;
∵x+y+(x+y)-z=8,而z=
,
∴x+y=
,
即四边形ABCD的面积为
.
 ∵BD:DC:BC=3:4:5,
∵BD:DC:BC=3:4:5,∴设BD=3λ,则DC=4λ,BC=5λ;
如图,将△ABD、△ACD分别沿AB、AC折叠,得到△ABE和△ACF;
则∠ABE=∠ABD,∠ACD=∠ACF;
AE=AD=4,AF=AD=4;∠EAB=∠DAB,∠FAC=∠DAC;
∵∠BAC=45°,
∴∠EAF=90°
∵∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,
∴∠ABC+∠ABE=180°,∠ACB+∠ACF=180°,
∴E、B、C、F四点共线;
∵∠EAF=90°,
∴△EAF为等腰直角三角形,
∴△AEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∵(3λ)2+(4λ)2=(5λ)2,
∴△BDC为直角三角形;
EF=3λ+4λ+5λ=12λ;
由勾股定理得:(12λ)2=42+42,
解得:λ=
| ||
| 3 |
| 2 |
4
| ||
| 3 |
∴△BDC的面积=
| 1 |
| 2 |
| 2 |
4
| ||
| 3 |
| 4 |
| 3 |
设△ABD、△ADC、△BDC的面积分别为x,y,z;
∵x+y+(x+y)-z=8,而z=
| 4 |
| 3 |
∴x+y=
| 14 |
| 3 |
即四边形ABCD的面积为
| 14 |
| 3 |
看了 如图,∠BAC=45°,BD...的网友还看了以下:
[小学奥数]计算四边形的面积把四边形ABCD的各边延长,使AB=BA',BC=CB',CD=DC' 2020-04-27 …
如图,在梯形abcd中,上底ab=3.6厘米,下底dc=4.8厘米.三角形甲比三角形乙大20平方厘 2020-05-01 …
高一数学关于向量的的问题》》》以下大写字母组合皆为向量:已知A、B、C、D为平面上四个互异点,且满 2020-05-15 …
四边形ABCD中,AD┴DC,AD=8,DC=6,CB=24,AB=26,则四边形ABCD的面积是 2020-05-16 …
点A.B.C在同一直线上,分别以AB.BC为边向外作等边三角形ABD,BCE,连接AE,DC.当A 2020-05-20 …
在三角形ABC中,D为AB边上一点,DA=DC.已知B=45度,BC=1(1)若DC=根号6/3, 2020-07-20 …
以等腰直角三角形ABC的斜边AB为边作等边三角形ABD,连接DC,以DC为边作等边三角形DCE,B 2020-07-30 …
已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、D 2020-08-03 …
、解:过P作PE⊥AB.∵四边形ABCD为正方形,∴AB=DC=AD=BC=8,∠B=90°,∠C= 2020-11-01 …
如图,图中的四边形都是正方形,三角形都是直角三角形,其中正方形的面积分别记为A、B、C、D,则它们之 2021-01-22 …