早教吧作业答案频道 -->数学-->
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.(Ⅰ)证明:AP∥平面BED;(Ⅱ)证明:平面APC⊥平面BED;(Ⅲ)若BC=PC=2,
题目详情
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.
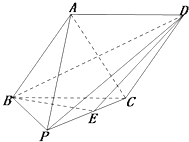
(Ⅰ)证明:AP∥平面BED;
(Ⅱ)证明:平面APC⊥平面BED;
(Ⅲ)若BC=PC=2,∠ABC=60°,求异面直线AP与BC所成角的余弦值.

(Ⅰ)证明:AP∥平面BED;
(Ⅱ)证明:平面APC⊥平面BED;
(Ⅲ)若BC=PC=2,∠ABC=60°,求异面直线AP与BC所成角的余弦值.
▼优质解答
答案和解析
(本小题满分13分)
证明:(Ⅰ)设AC∩BD=O,ABCD是平行四边形,故O为BD的中点,连结OE,
∵点E是PC的中点,∴AP∥OE,
OE⊂平面BED,AP⊄平面BED,
∴AP∥平面BED,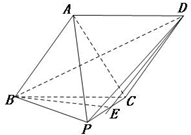
(Ⅱ)∵平面PBC⊥平面ABCD,∠PCB=90°,
故PC⊥平面ABCD,又BD⊂平面ABCD,∴PC⊥BD,
而底面ABCD是菱形,故AC⊥BD,
又AC∩PC=C,∴BD⊥平面APC,
∵BD⊂平面BED,
∴平面APC⊥平面BED.
(Ⅲ)由(Ⅰ)知BC∥AD,故∠PAD为异面直线AP与BC所成的角,
由已知BC=PC=2,∠ABC=60°,底面ABCD是菱形,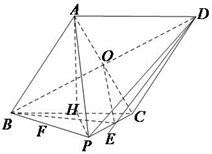
故AB=BC=AC=PC=2,
∴在Rt△DPC中,PC=DC=2,故DP=2
,
取BC中点H,则AH⊥BC,AH⊥平面PBC,
在Rt△AHP中,PH=
,AH=
,故AP=2
,
∴AP=2
,在△APD中,cos∠PDE=
=
.
∴异面直线AP与BC所成角的余弦值为
.
证明:(Ⅰ)设AC∩BD=O,ABCD是平行四边形,故O为BD的中点,连结OE,
∵点E是PC的中点,∴AP∥OE,
OE⊂平面BED,AP⊄平面BED,
∴AP∥平面BED,

(Ⅱ)∵平面PBC⊥平面ABCD,∠PCB=90°,
故PC⊥平面ABCD,又BD⊂平面ABCD,∴PC⊥BD,
而底面ABCD是菱形,故AC⊥BD,
又AC∩PC=C,∴BD⊥平面APC,
∵BD⊂平面BED,
∴平面APC⊥平面BED.
(Ⅲ)由(Ⅰ)知BC∥AD,故∠PAD为异面直线AP与BC所成的角,
由已知BC=PC=2,∠ABC=60°,底面ABCD是菱形,

故AB=BC=AC=PC=2,
∴在Rt△DPC中,PC=DC=2,故DP=2
| 2 |
取BC中点H,则AH⊥BC,AH⊥平面PBC,
在Rt△AHP中,PH=
| 5 |
| 3 |
| 2 |
∴AP=2
| 2 |
| ||
| AP |
| ||
| 4 |
∴异面直线AP与BC所成角的余弦值为
| ||
| 4 |
看了 如图,在四棱锥P-ABCD中...的网友还看了以下:
英语翻译四边形ABCD有外接圆的充要条件是$S=sqrt((p-a)*(p-b)*(p-c)*(p- 2020-03-31 …
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A、B、C、D路线运动, 2020-05-16 …
已知抛物线y=ax^2+bx+c与x轴交于原点O和点A(4,0),点P是第一象限内的抛物线上到两坐 2020-06-14 …
求证:四边形ABCD有外接圆的充要条件是S=√((p-a)*(p-b)*(p-c)*(p-d))其 2020-06-23 …
1.如图,过线段AB外一点P,引两条射线与AB相交于C、D,使C、D把线段AB三等分.题目中没有C 2020-06-27 …
关于海伦公式的推论三角形的是S=SQR[P(P-A)(P-B)(P-C)]圆内接四边形是S=SQR 2020-07-30 …
如图,A、B、C、D都在直线MN上,点P在直线外,若∠1=60°,∠2=90°,∠3=120°,∠ 2020-08-03 …
S²=(p-a)(p-b)(p-c)(p-d),其中p=½(a+b+c+d)这个公式怎么用S²=(p 2020-11-07 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …
关于化学平衡常数和浓度积的问题化学平衡常数:c^p(C)*c^q(D)/C^m(A)*c^n(B)浓 2021-01-22 …